Question
Question: An infinite non-conducting sheet of thickness \(d\) and contains uniform charge distribution of char...
An infinite non-conducting sheet of thickness d and contains uniform charge distribution of charge density ρ. Which one of the following graphs represents the variation of Electric Field Ex v/s x (Here x is the distance from the central plane of non-conducting sheet) and $0(A).
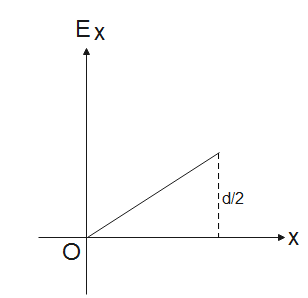
(B).
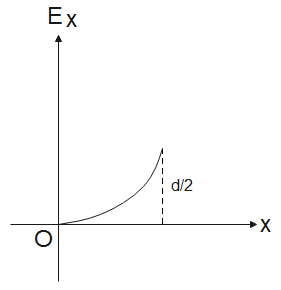
(C).
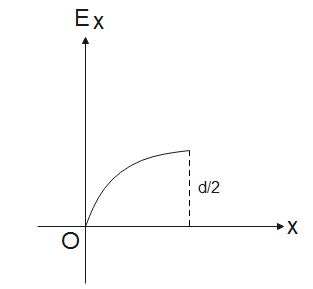
(D).
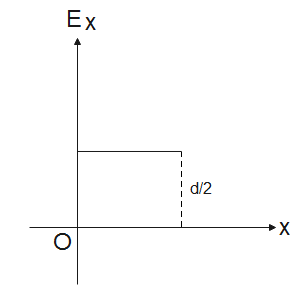
Solution
Flux is the amount of electric field lines passing per unit area. Hence, the flux is the integration of electric field vectors and area vectors. By the gauss law, flux is charge divided by absolute permittivity. Using both equations, we can determine the electric sheet due to the charged sheet which will also give us the relation between electric field and distance from the sheet.
Formulas used:
ϕ=∮E.dS
ϕ=ε0q
Complete answer:
We know that the flux through a surface is given by-
ϕ=∮E.dS - (1)
Here, ϕ is the flux passing through a surface
E is the electric field vector
S is the area vector
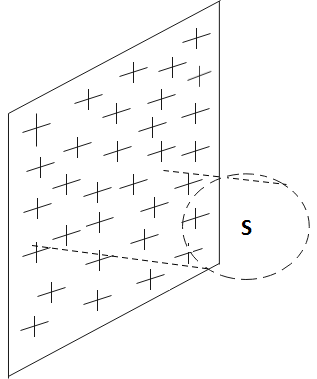
According to the gauss law, the flux passing through a surface will be-
ϕ=ε0q - (2)
Therefore, using eq (1) and eq (2), we have,
∮EdScos0=ε0q⇒E∮dS=ε0q
⇒ES=ε0q - (3)
We know that charge density is the charge per unit volume. Therefore,
ρ=area×thickness
⇒ρ=S×d - (4)
From eq (3),
⇒ES=ε0q⇒E=Sε0q⇒E=Sdε0qd
Substituting from eq (4) in the above equation,
⇒E=ρε0qd
The electric field due to the infinite non-conducting sheet of thickness d is ρε0qd. It is independent of x or the distance from the centre of the sheet; this means the field remains uniform throughout.
Therefore, the electric field due to a charged sheet is ρε0qd, it is independent of x.
Hence, the correct option is (D).
Note:
The electric field is a vector quantity and its direction is the direction in which positive charge flows. The dot product of two vectors gives a scalar quantity. The charge distribution can also be represented by surface charge density, it is the charge per unit area. The electric field due to a charged sheet will be the same at any distance from the centre of the sheet.
