Question

An infinite cylinder of radius ${{r}_{0}}$ carrying linear charge density $\lambda$. The equation of the equipotential surface for this cylinder is

& \text{A}\text{. }r={{r}_{0}}{{e}^{\pi {{\varepsilon }_{0}}\left[ V\left( r \right)+V\left( {{r}_{0}} \right) \right]\lambda }} \\\ & \text{B}\text{. }r={{r}_{0}}{{e}^{\pi {{\varepsilon }_{0}}\left[ V\left( r \right)+V\left( {{r}_{0}} \right) \right]{{\lambda }^{2}}}} \\\ & \text{C}\text{. }r={{r}_{0}}{{e}^{-2\pi {{\varepsilon }_{0}}\left[ V\left( r \right)+V\left( {{r}_{0}} \right) \right]/\lambda }} \\\ & \text{D}\text{. }r={{r}_{0}}{{e}^{-2\pi {{\varepsilon }_{0}}\left[ V\left( r \right)+V\left( {{r}_{0}} \right) \right]\lambda }} \\\ \end{aligned}$$

Answer 1

Define Gauss’s theorem. Consider a cylindrical gaussian surface with radius r and length L. Find the net flux through the gaussian surface. Obtain the relation between the potential and electric field. Obtain the equation for the equipotential surface from the above equation.

Complete step by step solution:
We have an infinitely long cylinder of radius ${{r}_{0}}$ carrying a charge density $\lambda$.

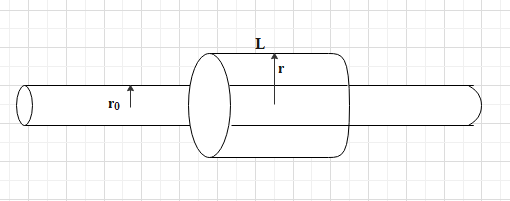
Consider a gaussian surface around a cylinder of radius ${{r}_{0}}$ and length L.
Now, from gauss’s theorem we can write that,
$\int{E.ds=\dfrac{\lambda L}{{{\varepsilon }_{0}}}}$
Where, $\lambda L$ is the net charge enclosed by the gaussian surface of radius r and length L.
We can simplify this integration as,
$\begin{aligned} & {{E}_{r}}.2\pi rL=\dfrac{\lambda L}{{{\varepsilon }_{0}}} \\\ & {{E}_{r}}=\dfrac{\lambda }{2\pi r{{\varepsilon }_{0}}} \\\ \end{aligned}$
Now, the potential can be found out as,
$\Delta V=-\int{E.dl}$
Here, we need to find the potential from the radius of the cylinder r to radius of the gaussian surface ${{r}_{0}}$ .
So, we can write that,
$\begin{aligned} & V\left( r \right)-V\left( {{r}_{0}} \right)=-\int\limits_{{{r}_{0}}}^{r}{E.dl} \\\ & V\left( r \right)-V\left( {{r}_{0}} \right)=-\int\limits_{{{r}_{0}}}^{r}{\dfrac{\lambda }{2\pi r{{\varepsilon }_{0}}}dr} \\\ & V\left( r \right)-V\left( {{r}_{0}} \right)=-\dfrac{\lambda }{2\pi {{\varepsilon }_{0}}}\int\limits_{{{r}_{0}}}^{r}{\dfrac{1}{r}dr} \\\ & V\left( r \right)-V\left( {{r}_{0}} \right)=-\dfrac{\lambda }{2\pi {{\varepsilon }_{0}}}\left[ \ln r \right]_{{{r}_{0}}}^{r} \\\ & V\left( r \right)-V\left( {{r}_{0}} \right)=-\dfrac{\lambda }{2\pi {{\varepsilon }_{0}}}\left[ \ln r-\ln {{r}_{0}} \right] \\\ & -\left[ V\left( r \right)-V\left( {{r}_{0}} \right) \right]\dfrac{2\pi {{\varepsilon }_{0}}}{\lambda }=\ln \left[ \dfrac{r}{{{r}_{0}}} \right] \\\ & \dfrac{r}{{{r}_{0}}}={{e}^{-\left[ V\left( r \right)-V\left( {{r}_{0}} \right) \right]\dfrac{2\pi {{\varepsilon }_{0}}}{\lambda }}} \\\ & r={{r}_{0}}{{e}^{-2\pi {{\varepsilon }_{0}}\left[ V\left( r \right)-V\left( {{r}_{0}} \right) \right]/\lambda }} \\\ \end{aligned}$
So, the equation for equipotential surface of the infinite long cylinder is $r={{r}_{0}}{{e}^{-2\pi {{\varepsilon }_{0}}\left[ V\left( r \right)-V\left( {{r}_{0}} \right) \right]/\lambda }}$

The correct option is (C).

Additional information: An equipotential surface can be defined as a surface over which the potential is constant at every point on the surface. The potential difference between two points on the surface will always be zero.
Gauss’s theorem can be defined as the net flux through a closed surface is directly proportional to the net charge in the volume enclosed by a closed surface.

Note: Using the gauss’s theorem we can prove many things. We can find the electric field due to the current carrying conductor of every shape using Gauss's theorem. From Gauss’s theorem, we can also find the potential from the relation of potential and electric field.