Question
Question: An inductor of inductance \(L=\dfrac{\tau R}{2}\) and a resistor of resistance \(R\) is connected to...
An inductor of inductance L=2τR and a resistor of resistance R is connected to a battery of emf V as shown in the figure. The potential difference across the resistance at a time t=τln2 after the switch S is closed is kV . Find the value of k (τ is constant)
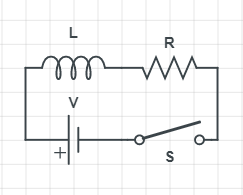
Solution
Here, we have an LR series circuit, to find the potential difference across R at some time t, we need to first calculate the total current in the circuit at any time, and then find the potential difference across the resistance R. then if we substitute the value of t and equate the answer to kV, we can find the value of k.
Formula used:
i=RV1−e−LRt
Complete step by step answer:
Let i be the current in the circuit, clearly it depends on the time, as there is an inductor in the circuit. Then the total current is expressed as i=ir+(ir−ii)e−LRt.
Where, ir is the current flowing through the resistorR, il is the current flowing through the inductor L in time t.
Also τ is the time constant and it is given as τ=RL
Here, it is given that, inductance L=2τR, resistance isRand an emf Vis applied to the circuit, then from ohm’s law, we can write the ir=RV.
If ii=0, then we get, i=RV−RVe−LRt=RV1−e−LRt
⟹Vr=V1−e−LRt, where Vr is the voltage across the resistance R and is given as,Vr=iR
From, L=2τR
Rearranging, we get,RL=2τ
Substituting, in the above, we get, Vr=V1−e−τ2t
We need to find the potential difference across the resistance at a time t=τln2 , hence substituting for in the above equation,
we get, Vr=V1−e−τ2τln2
⟹Vr=V(1−e−2ln2)
⟹Vr=V(1−e−ln4)
⟹Vr=V(1+4)
⟹Vr=5V
Given that Vr=kV
Then, we get kV=5V
⟹k=5
Hence the value of k is 5
Note:
τ is the value at which RV is the final steady state current flowing through the circuit, it is reached at 5τ. Also, after reaching this steady state current, the inductance of the coil reduces to zero. In a charging circuit, 5τ is called the transient time of the circuit.
