Question

An inductor may store energy in:
A) its electric field
B) its coil
C) its magnetic field
D) both electric and magnetic fields

Answer 1

The question is based on the self-inductance of an inductor and the energy stored in it. An inductor, also called a coil, chokes, or reactor, is a passive two-terminal electrical component that stores energy in a magnetic field when electric current flows through it. The working principle is the electromagnetic induction.

Complete step by step solution:
Step 1:

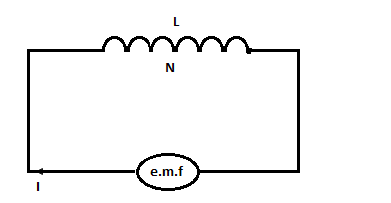
For self-inductance of inductor the general equation is,

$\Rightarrow N\phi = LI$----- (1)

Where, $N =$number of turn in the coil; $\phi =$magnetic flux; $L =$self-induction coefficient of the inductor; $I =$current flowing through the coil.

Step 2: Now differentiate equation (1) with respect to time$\left( t \right)$, we get,

$\Rightarrow N\dfrac{{d\phi }}{{dt}} = L\dfrac{{dI}}{{dt}}$[Since $N$and $L$are constant with respect to time]

Since, $\Rightarrow e.m.f = N\dfrac{{d\phi }}{{dt}}$

$$\Rightarrow$$$e.m.f = L\dfrac{{dI}}{{dt}}$ ---------- (2)

Step 3: Let work done by the inductor to store $dq$amount charge in time $dt$is given by,

$\Rightarrow dW = e.m.f \times dq$

Substituting the value of $e.m.f$ from equation (2) we get,

\Rightarrow $$$dW = L\dfrac{{dI}}{{dt}}dq$ \Rightarrow dW = L\dfrac{{dI}}{{dt}}Idt$ [Since,$I = \dfrac{{dq}}{{dt}}$] $$ \Rightarrow dW = LIdI$

Step 4: Total work done by the conductor to store current up to $I$is given by,
$\Rightarrow \int\limits_0^I {dW = } \int\limits_0^I {LIdI}$
$\Rightarrow W = L\int\limits_0^I {IdI}$
$\Rightarrow W = L\dfrac{{{I^2}}}{2}$

Therefore, the energy stored by the inductor is equal to the work done by the inductor.
Thus, an inductor may store energy in its magnetic field.

Option (C) is the correct answer.

Note: student should familiar with the result value that is energy stored, $E = L\dfrac{{{I^2}}}{2}$where $L =$self-induction coefficient of the inductor; $I =$current flowing through the coil. And also remember the equation of the inductor that is $N\phi = LI$where, $N =$number of turns in the coil; $\phi =$magnetic flux.
An inductor is a passive electronic component which is capable of storing electrical energy in the form of magnetic energy. Basically, it uses a conductor that is wound into a coil, and when electricity flows into the coil from the left to the right, this will generate a magnetic field in the clockwise direction.
Like an inductor , capacitors also store energy.