Question

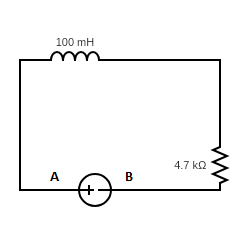
An inductor L = 100mH, a resistor R = 100(Ohms) and a battery E = 100V are initially connected in series as shown in the figure. After a long time the battery is disconnected after short circuiting the points A and B. The current in the circuit after 1ms is.

1. 1 A
2. $\dfrac{1}{e}$A
3. e A
4. 0.1 A

Answer 1

Here there will be two equations formed one when the battery is connected and another when there is no battery and the circuit is short circuited. Here we use ohm's law and the formula for inductive resistance.

Formula used:
Energy in the circuit =$\dfrac{1}{2}L{(\dfrac{E}{R})^2}$;
Where:
L = Inductance;
E = Source battery.
R = Resistance.
Ohm’s law
$I = \dfrac{E}{R}$;
I = Current.
E = Voltage source.
R = Resistance.
Inductive Resistance
$i = {I_o}{e^{\dfrac{{ - tR}}{L}}}$;
Where:
i = Current;
${I_o}$= I = Initial current.
t = time.
R = Resistance.
L = Inductance.

Complete answer:
The formation of an electrical circuit happens when a path that is of a conductive nature is created. The conductive path allows a number of charges to move continuously and this continuous movement is called current. There is a law which relates current “I”, voltage “V” and Resistance “R”. The law is known as Ohm’s Law. It states that the amount of electric current flowing in the circuit is proportional to the voltage across it and is inversely proportional to the resistance.
Write Ohm’s Law:
${I_o} = \dfrac{E}{R}$;
Apply the formula and find out the initial current;
Equation for inductive resistance is:
$i = {I_o}{e^{\dfrac{{ - tR}}{L}}}$;
Now, put the value ${I_o} = \dfrac{E}{R}$(Ohm’s Law) in the above equation and solve,
$i = \dfrac{E}{R}{e^{\dfrac{{ - tR}}{L}}}$;
Put the given value in the above equation:
$i = \dfrac{{100}}{{100}} \times {e^{\dfrac{{ - {{10}^{ - 3}} \times {{10}^2}}}{{100 \times {{10}^{ - 3}}}}}}$;
Do the mathematical calculation in the above equation by dividing the numerator with denominator:
$i = {e^{ - 1}}Ampere$ ….(The unit of current is Amperes)

Option”2” is correct. The current in the circuit after 1ms is $i = eA$.

Note:
Here we have to apply the relation between ohm's law and formula for inductive resistance. Put the value of current which is found out by using ohm's law in the formula for inductive resistance. Make sure to do the mathematical calculations carefully.