Question

An incompressible non-viscous fluid flows steadily through a cylindrical pipe which has radius 2R at point A and radius R at point B farther along the flow direction. If the velocity of the fluid at a point A is V, its velocity at the point B will be:

Answer 1

Hint: In fluid dynamics the continuity equation explains the rate at which the mass enters the system is equal to the ass that leaves the system.

Complete step by step answer:
We can consider a liquid flowing through a pipe. Let ${{\text{A}}_{\text{1}}}{\text{and}}{{\text{A}}_{\text{2}}}$ be the areas of cross-sections at point A and B respectively.

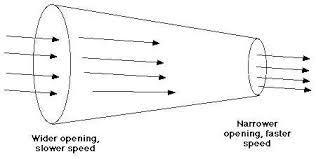
Let the liquid enter with velocity ${{\text{v}}_1}$ at A and leave with velocity ${{\text{v}}_2}$at B. volume of liquid entering the tube $= {{\text{A}}_1}{{\text{v}}_1}$ and volume of liquid leaving the tube ${\text{ = }}{{\text{A}}_2}{{\text{v}}_2}$. Since the same volume of liquid flows across each section of the tube in unit time, we have
${{\text{A}}_1}{{\text{v}}_1} = {{\text{A}}_2}{{\text{v}}_2}$
This expression is called the equation of continuity for steady flow of an in-compressible, non-viscous liquid. From this equation it follows that the velocity of flow is small, where the cross-sectional area is large and the velocity of flow is large where the cross-sectional area is small.
Given, At point A, radius ${r_1} = 2R$
Now the Velocity, ${{\text{v}}_{\text{1}}} = {\text{V}}$
At point B, radius ${r_2} = R$ . Velocity, ${{\text{v}}_2} = ?$
According to equation of continuity,
${{\text{A}}_{\text{1}}}{{\text{V}}_{\text{1}}}{\text{ = }}{{\text{A}}_{\text{2}}}{{\text{V}}_{\text{2}}}$
${V_2} = \dfrac{{{A_1}}}{{{A_2}}} \times {V_1} = \dfrac{\pi {r_1}^2}{\pi {r_2}^2} \times V$
${{\text{V}}_2} = \dfrac{{{{\left( {2R} \right)}^2}}}{{{{\left( R \right)}^2}}} \times {\text{V}}$
${{\text{V}}_2} = \dfrac{{4{R^2}}}{{{{\left( R \right)}^2}}} \times {\text{V = 4V}}$
Hence, velocity at point B is 4V.

Additional information:
If fluid flows such that its velocity at a point is always the same in magnitude and direction, the fluid is said to have streamlined flow. Streamline flow is also known as steady flow or orderly flow. Consider a liquid flowing through a pipe of the shape. A particle of the liquid possesses velocity $v_1$ at A and $v_2$ at B and $v_3$ at C. as the liquid flows, different particles will pass through points A, B, and C. If it so happens that all the particles will have velocity $v_1$ when they reach A, velocity $v_2$ when they reach B and velocity $v_3$ when they reach C, then the flow of the liquid is orderly and is called streamline flow.

Note: The continuity equation provides useful information about the flow of fluids and their behavior in the flow of pipe or hose. This equation describes how a fluid conserves a mass in its equation.