Question

An incompressible fluid flows steadily through a cylindrical pipe which has a radius $2R$ at point $A$ and radius $R$ at point $B$ along the flow direction. If the velocity of liquid flow at $A$ is $\nu$, its velocity at point $B$ is?
A. $2\nu$
B. $\nu$
C. $\dfrac{\nu }{2}$
D. $4\nu$

Answer 1

For fluid flowing through a pipe we use a continuity equation that is $\rho {A_1}{\nu _1} = \rho {A_2}\nu {}_2$, where ${A_1}$ ${A_2}$ are the area of cross-section and ${\nu _1}$ , ${\nu _2}$ are the velocity of the liquid, and $\rho$ is the density of the liquid. The area of a circle is $\pi {r^2}$ where $r$ is the radius of the circle. Putting the values from the question in the above relation we will find the velocity of the liquid flowing at $B$.

Complete step by step answer:

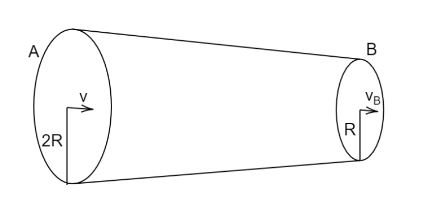
At point $A$ radius is $2R$ and velocity of liquid flow is $\nu$. At point $B$ radius is $R$ and let velocity be ${\nu _B}$. Using the equation of continuity (The continuity equation is defined as the product of the cross-sectional area of the pipe and the velocity of the fluid at any given point along the pipe is constant.)
$\rho {A_1}{\nu _1} = \rho {A_2}\nu {}_2$
The density of the liquid is constant throughout the flow so
${A_1}{\nu _1} = {A_2}\nu {}_2$
Cross-sectional area at a point $A$ is $\pi {\left( {2R} \right)^2}$ and at a point $B$ is $\pi {\left( R \right)^2}$ putting these values in above equation we get
$\Rightarrow \pi {\left( {2R} \right)^2} \times \nu = \pi {\left( R \right)^2} \times {\nu _B}$
$\therefore {\nu _B} = 4\nu$

Hence option D is the correct answer.

Note: If the fluid is incompressible, the density will remain constant for steady flow.We can also solve this as we know for the fluid flowing through a pipe the velocity of a fluid is inversely proportional to the area of the cross-section that is $\nu \propto \dfrac{1}{A}$. Therefore we will get $\dfrac{{{\nu _B}}}{\nu } = \dfrac{{{A_1}}}{{{A_2}}}$ putting the values from the question we can find ${\nu _B}$.