Question

An inclined plane making an angle of 30° with the horizontal is placed in a uniform electric field E = 100V/m. A particle of mass 1 kg and charge 0.01 c is allowed to slide down from rest from a height of 1m. If the coefficient of friction is 0.2 the time taken by the particle to reach the bottom is 330x, then find the value of x.

Answer 1

The particle is charged, so it will experience the electric force. But due to being inclined, we will have to resolve the force. Also, because of the friction when the particle comes down, frictional force acts on the body and it always opposes the motion of the body. Also, the weight of the body will have to be resolved.

Complete step by step solution:
We draw the diagram representing all the forces.

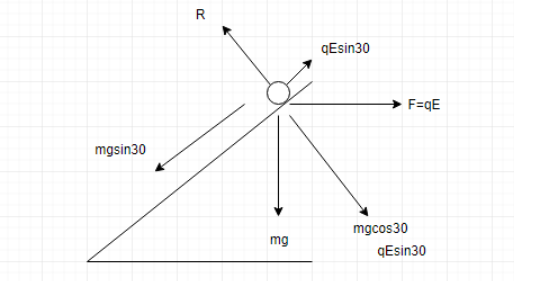
The net forces act down the plane.
For forces in the horizontal:
$F\text{ }=\text{ }mg\text{ }sin\text{ }30\text{ }\text{ }\mu R\text{ }\text{ }qE\text{ }cos\text{ }30$--(1)
There is no motion in the vertical direction, so, $R=mg\cos 30+qE\sin 30$
Putting the value of R in equation (1) we get,
$F\text{ }=\text{ }mg\text{ }sin\text{ }30\text{ }\text{ }\mu (mg\cos 30+qE\sin 30)\text{ }\text{ }qE\text{ }cos\text{ }30$
But from Newton’s second law,$F=ma$
$\Rightarrow \text{a }=\text{ }g\text{ }sin\text{ }30\text{ }\text{ }\mu g\cos 30+\dfrac{qE}{m}\sin 30\text{ }\dfrac{\text{ }qE}{m}\text{ }cos\text{ }30$
Substituting the value, we get,
$\Rightarrow \text{a }=\text{ 10}\times \dfrac{1}{2}\text{ }\text{ 0}\text{.2}\times 10\times \dfrac{\sqrt{3}}{2}+\dfrac{0.01\times 100}{1}\times \dfrac{1}{2}\text{ }\dfrac{\text{ 0}\text{.01}\times 100}{1}\text{ }\times \dfrac{\sqrt{3}}{2}$\
$\therefore a=2.24m/{{s}^{2}}$--(2)
Now it was given that the height of the plane 1m.
Using trigonometry,
\Rightarrow \sin 30=\dfrac{P}{H} \\\ \Rightarrow \dfrac{1}{2}=\dfrac{1}{H} \\\ \therefore H=2m \\\
So, the distance covered is$2m$, now to find the time we can make use of equation of motion. Initially it was at rest, thus,
\Rightarrow s=\dfrac{a{{t}^{2}}}{2} \\\ \Rightarrow 4=2.24{{t}^{2}} \\\ \Rightarrow {{t}^{2}}=1.75 \\\ \therefore t=1.33s \\\
But the time given was $330x$,
$\therefore 330x=1.33$
So, $x=0.004$

Note: While solving such problems we need to find first all the forces acting. We then have to see in which direction the body is moving. Here the body was moving along the plane but there was no motion in the vertical direction. So, we just have to balance all the forces in a particular direction. On an incline the weight is always balanced by the normal reaction.