Question

An inclined plane making an angle of ${30^ \circ }$with the horizontal electric field of $100V{m^{ - 1}}$ as shown in Figure. A particle of mass $1kg$ and charge $0.01C$is allowed to slide down from rest from a height of $1m$. If the coefficient of friction is 0.2. The time is $330x$millisecond, it will take the particle to reach the bottom. Then find $x$

Answer 1

Hint From the given diagram, draw the free body diagram of the particle on the inclined surface. The particle will slip down, which makes it undergo frictional force and normal. Find the force value, using which find the acceleration value. Substitute the acceleration value in the second equation of motion and find out t.

Complete Step By Step Solution
According to the diagram, we have an electric charge placed on an inclined plane with its horizontal electric field of $100V{m^{ - 1}}$. Since the direction of electric field with respect to the plane isn’t provided, let us assume that the direction of electric field is along the direction of the inclined plane.
Let’s draw the free body diagram of the charge and find out its forces.

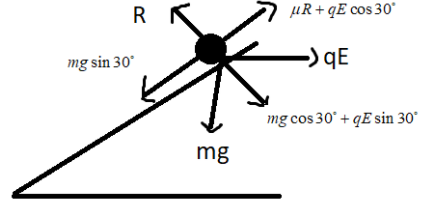
The particle experiences a normal force mg. The particle experiences a force $qE$, perpendicular to the reaction due to the presence of a horizontal electric field. Due to inclination, it experiences 2 forces namely$qE\cos {30^ \circ }$ and $qE\sin {30^ \circ }$.
Now force f experienced by the charge is given as ,
$f = mg\sin {30^ \circ } - (qE\cos {30^ \circ } + \mu R)$, where f is considered along the line of inclination
$\Rightarrow f = mg\sin {30^ \circ } - (qE\cos {30^ \circ } + \mu (mg\cos {30^ \circ } + qE\sin {30^ \circ }))$(From the above diagram, we can conclude that $R = mg\cos {30^ \circ } + qE\sin {30^ \circ }$)
Substituting the given values on the above equation we get,
$\Rightarrow f = (1 \times 9.8 \times 0.5) - ((0.01 \times 100 \times \dfrac{{\sqrt 3 }}{2}) + [0.2 \times (1 \times 9.8 \times \dfrac{{\sqrt 3 }}{2} + (0.01 \times 100 \times 0.5))])$
Simplifying further we get,

\\\ \Rightarrow f = (1 \times 9.8 \times 0.5) - ((0.01 \times 100 \times \dfrac{{\sqrt 3 }}{2}) + [0.2 \times 8.986]) \\\ \end{gathered} $$ $$ \Rightarrow f = (1 \times 9.8 \times 0.5) - (0.866 + 1.7972)$$ $$ \Rightarrow f = 2.24N$$ Now, we know the mass and force experienced by the charge. Using this, we can find the acceleration of the particle, $$a = \dfrac{f}{m}$$ $$ \Rightarrow a = \dfrac{{2.24}}{1} = 2.24m{s^{ - 2}}$$(Since, $$1N/kg = 1m{s^{ - 2}}$$) Now, using the second equation of motion, we know that height s is given and we have found out acceleration value. Substituting this in second equation of motion we get, $$s = ut + \dfrac{1}{2}a{t^2}$$ Here the total displacement s of the charge is not directly given , since the plane is inclined by $${30^ \circ }$$. Height of the particle is given and we need to find the length l of the inclined plane, which can be done using, $$\sin {30^ \circ } = \dfrac{h}{l}$$ $$ \Rightarrow l = \dfrac{h}{{\sin {{30}^ \circ }}} = 2m$$ Substituting this for s in the above equation, we get $$ \Rightarrow 2 = 0 \times t + \dfrac{1}{2}(2.24){t^2}$$ $$ \Rightarrow 4 = (2.24){t^2}$$ $$ \Rightarrow {t^2} = 1.6393$$ $$ \Rightarrow {t^{}} = 1.33s$$ We know $${t^{}} = 330x$$ Hence , $$ \Rightarrow x = t/0.33$$ $$ \Rightarrow x = 1.44s$$ **Note** Normal force is defined as the force which is exerted by the surface to prevent objects and particles from passing each other. It is a support force exerted by the surface on the object while it is in contact with the surface.