Question

An incident ray strikes a plane mirror at an angle of $15{}^\circ$ with the mirror. The angle between the incident ray and reflected ray is equal to:
$\begin{aligned} & A.\text{ 15}{}^\circ \\\ & B.\text{ 30}{}^\circ \\\ & C.\text{ 150}{}^\circ \\\ & D.\text{ 90}{}^\circ \\\ \end{aligned}$

Answer 1

The question has been provided with an angle between interface and incident ray which is nothing but glancing angle, given as $15{}^\circ$. We know that the angle between horizontal plane of interface and normal is $90{}^\circ$, Hence calculate angle of incident. Whereas angle of incidence is equal to the angle of reflection hence calculate angle between them.

Complete step by step answer:

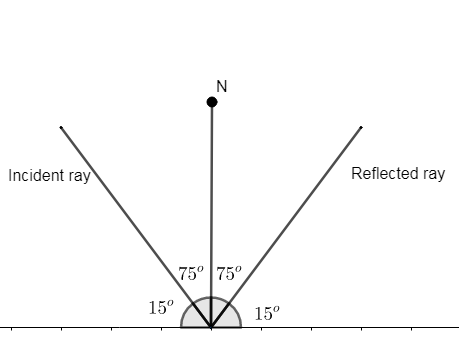
The question is stated as a ray incident on a plane mirror: When a ray of light is incident on a plane mirror it gets reflected back. It has given that an incident ray strikes a plane mirror at an angle $15{}^\circ$ with the mirror. This is nothing but glancing angle. The glancing angle $\left( {{\theta }_{g}} \right)$ is nothing but an angle made by incident ray with the reflecting surface or interface, which is denoted as ${{\theta }_{g}}$ and it is given as,
${{\theta }_{g}}=15{}^\circ$
We know that, when ray strikes on an interface it makes an angle with normal, the angle between incident ray and normal is nothing but an angle of incidence which is denoted by i. Whereas, normal is the perpendicular draw to the interface which is denoted by N.
Since N is perpendicular to interface i.e. plane mirror then angle between horizontal surface of plane mirror and normal must be $90{}^\circ$. So we can also write it as, sum of glancing angle and incident angle is equal to $90{}^\circ$, mathematically,
$\angle i+\angle \theta g=90{}^\circ$
Put value of glancing angle $\theta g$
$\begin{aligned} & \angle i+15{}^\circ =90{}^\circ \\\ & \angle i=90{}^\circ -15{}^\circ \\\ & \angle i=75{}^\circ .........\left( 1 \right) \\\ \end{aligned}$
This is the angle of incidence. We know that, when ray incident on a plane mirror, it reflects back on the opposite side of normal, the angle made between normal and reflected ray is called angle of reflection. In the case of a plane mirror, the angle of incidence is equal to the angle of reflection. i.e., $\angle i=\angle r$
Where $\angle r$ = angle of reflection.
From (1),
$\angle r=75{}^\circ$. This is an angle of reflection. Now, we have asked to find angle between incident ray and reflected ray,
$i.e.\text{ }\angle \text{i+}\angle \text{r=75}{}^\circ +75{}^\circ =150{}^\circ$
Hence, the angle between the incident ray and reflected ray is equal to$150{}^\circ$.

So, the correct answer is “Option C”.

Note: The angle between incident ray (the original path) and reflected ray or refracted ray is called as the respective angle of deviation. So do not get confused between angle of glancing and respective angle of deviation. In this case interface is smooth, if the interface is rough then scattering will occur and in case of scattering, angle of incidence is not equal to angle of reflection