Question

An impulse $J$ is applied on a ring of mass $m$ along a line passing through its center O. The ring is placed on a rough horizontal surface, the linear velocity of center of ring once it starts rolling without slipping is:

(A) $\dfrac{J}{m}$
(B) $\dfrac{J}{{2m}}$
(C) $\dfrac{J}{{4m}}$
(D) $\dfrac{J}{{3m}}$

Answer 1

Hint : Here, the impulse is applied to a ring along the line passing through its center O. First of all we have to understand that impulse is a certain amount of force you apply for a certain amount of time to cause a change in momentum. So we have to equate the initial angular momentum and final angular momentum and then calculate the required linear velocity when the ring is in pure rolling.

Complete Step By Step Answer:
let us consider the figure above and mentioning some of the key aspects that can be useful for our calculation as below:

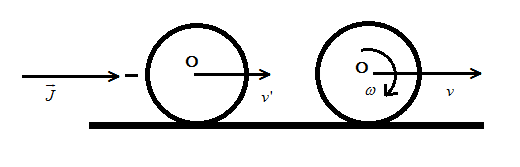
So let $v'$ be the velocity of the ring just after the impulse is applied to the ring.
i.e. initial velocity will be $u = 0$ and initial momentum ${p_{initial}} = 0$
And final momentum is given by: $p' = mv'$
$\because impulse = p' - {p_{initial}}$
We have,
$\Rightarrow J = mv' - 0$
$\Rightarrow J = mv'$
$\therefore v' = \dfrac{J}{m}$ …. $\left( 1 \right)$
But the ring is later starting to purely roll about the point it’s touching the surface, so the angular momentum of the ring about that point is conserved.
Thus, ${L_{initial}} = {L_{final}}$ or ${L_i} = {L_f}$ …. (Here, $L$ represents angular momentum) $\left( 2 \right)$
Now, initial and final angular momentum is given by:
${L_i} = mv'r$ ; $m$ is the mass of the ring and $r$ is the radius of the ring.
${L_f} = \left( {{I_{COM}} + m{r^2}} \right)\omega$ ; ${I_{COM}}$ along the center of mass of the ring, $\left( {{I_{COM}} + m{r^2}} \right)$ along the point its touching to the horizontal surface.
Thus, placing these value in equation $\left( 2 \right)$ we get
$\Rightarrow mv'r = \left( {{I_{COM}} + m{r^2}} \right)\omega$ …. $\left( 3 \right)$
Now, consider $v$ as the linear velocity of the ring when it starts pure rolling.
$\therefore v = \omega r \Rightarrow \omega = \dfrac{v}{r}$
Now, placing this value in equation $\left( 3 \right)$ we get
$\Rightarrow mv'r = \left( {m{r^2} + m{r^2}} \right)\dfrac{v}{r}$ …. $\left( {\because {I_{COM}} = m{r^2}} \right)$
Now, on equating the above equation we get,
$\Rightarrow v'r = 2{r^2}\dfrac{v}{r}$
$\Rightarrow v = \dfrac{{v'}}{2}$
$\Rightarrow v = \dfrac{J}{{2m}}$ …. (From $\left( 1 \right)$ )
Thus, the linear velocity of the ring after the pure rolling is obtained as $\dfrac{J}{{2m}}$ .
The correct answer is option B.

Note :
Here, it is important to understand what the problem is saying and also the great clarification between impulse and momentum relations as we have observed above is change in momentum. Angular momentum is about the center of mass of the rolling body when it’s rolling with angular velocity $\omega$ . Be careful while putting the values of the terms.