Question

An image is formed at a distance of 10 cm from the pole of the concave mirror of focal length 20 cm. Find the reinsertion of image.

Answer 1

Clearly the information that we have at our hands is the focal length and the image distance for the concave mirror so, all we need to do here is to find the distance of the object from the mirror (or pole).
Formula used:
For the case of spherical mirrors the relation between focal length f, object distance u and image distance v is:
$\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v}$.

Complete answer:
We are given that the image is formed at a distance of 10 cm from the pole of a concave mirror, so v = 10 cm and focal length of the concave mirror is f = - 20 cm. This means that our image forms between focus and pole. Well this seems like an absurd case if we take an image to form in front of the mirror, so we assume the image to form behind the mirror.
This can be visualized with the help of the following diagram:

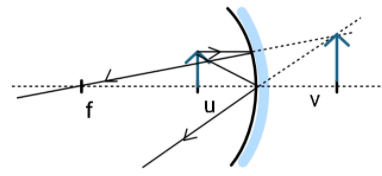
We can find the object placement as:
$\dfrac{1}{f} - \dfrac{1}{v} = \dfrac{1}{u}$.
In this, we take the LCM of the LHS and take inverse on both sides to get,
$u = \dfrac{v f}{v -f}$.
Now, all we need to do is keep the values at required places so we obtain the object distance to be:
$u = \dfrac{(10) \times (-20)}{(10) -(-20)} = - \dfrac{200}{3} = - 6.667 cm$.
Therefore as the object is kept at a distance of 6.667 cm from the pole the image will be formed at 10 cm distance behind the mirror.

Note:
We just assumed that the images formed behind the mirror instead of considering the case when the image would be formed in front of the mirror. It was a logical assumption because as we were given the image distance to be less in magnitude to the focal length there was only one scenario where this could happen and it was when the image formed would be behind the mirror.