Question
Question: An ideal monoatomic gas is carried around the cycle ABCDA as shown in the figure. The efficiency of ...
An ideal monoatomic gas is carried around the cycle ABCDA as shown in the figure. The efficiency of the gas cycle is
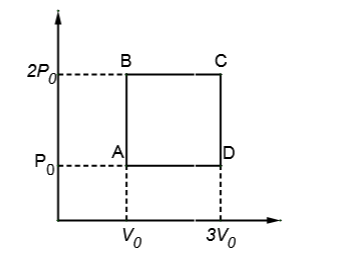
Solution
Hint: Efficiency of gas is the ratio of work done by gas to the total heat given to gas multiplied by 100. We can calculate work by calculating the area under curve and heat can be calculated using the first law of thermodynamics for every process.
Complete Step By Step Solution:
The efficiency of gas going through a cyclic process is given by
η=HinW×100,
where η is efficiency of gas, W is work done by gas and Hin is the heat given to gas in the entire process.
For calculating work done by cyclic processes we can just calculate the area under P-V graph (because work done by gas in integral of P with respect to V i.e. area under P-V curve)
Work done for process AB=0, as the area under AB curve is zero
Work done for process BC=3P0V0 , as this is the area under BC curve (area between curve and x-axis)
Work done for process CD=0, as the area under AB curve is zero
Work done for process DA=−P0V0 , as this is the area under DA curve (area between curve and x-axis) and the minus sign shows that volume is decreasing.
So the total work done for
AB+BC+CD+DA=0+3P0V0+0−P0V0=2P0V0
Now we have to calculate heat given to the system. From the first law of thermodynamics we know that heat given to a gas is equal to the sum of change in its internal energy and the work done by it.
Change in internal energy is given by
2f(PfVf−PiVi)=2f(ΔPV) , where f is freedom of degree of gas.
For a monoatonic gas freedom of degree is 3
Heat given for process AB
0+23(3P0V0−P0V0)=23×2P0V0=3P0V0
Heat given for process BC
3P0V0+23(3P0×2V0−3P0V0)=7.5P0V0
Heat given for process CD
0+23(P0×2V0−3P0×2V0)=−6P0V0
Heat given for process DA
−P0V0+23(P0V0−P0×2V0)=−2.5P0V0
This negative sign indicates heat is released, but we have to calculate total heat given so we will calculate sum of positive heat given only
Hin=7.5P0V0+2P0V0=10.5P0V0
So,
η=10.5P0V02P0V0×100=19.05
Note: The negative sign for heat indicates that the heat is released. But this heat is often not utilized. It is the energy wasted. For efficiency of any gas to increase we need heat released to be as low as possible. We want all the heat given to get converted into work.
