Question
Question: An ideal massless spring \(S\) can be compressed \(1{\text{ m}}\) by a Force of \(100{\text{ N}}\)in...
An ideal massless spring S can be compressed 1 m by a Force of 100 Nin equilibrium. The same spring is placed at the bottom of a frictionless inclined plane inclined at 30∘ to the horizontal. A 10 kgblock M is released from rest at the top of the incline and is brought to rest momentarily after compressing the spring by 2 m. If g=10 ms−2, what is the speed of mass just before it touches the spring?
A. 20 ms−1
B. 30 ms−1
C. 10 ms−1
D. 40 ms−1
Solution
Apply law of conservation of energy – Energy can neither be created nor be destroyed it can only be transformed from one form to another. The energy of an isolated system remains constant. Energy is never lost from the system, it just gets converted into some other form.
Complete step by step answer:
According to Hooke’s law, change in length of the spring is directly proportional to the force applied.Let us find out the spring constant.
F=kx
where F is the force applied, x is the change in the length of the spring and k is the
spring constant.
k=xF ⇒k=1100 ⇒k=100 N/m
From the diagram,
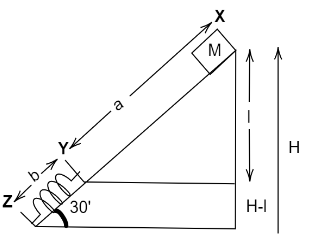
sinθ=(a+b)H…(i)
Applying Energy Conservation Principle,
The sum of Kinetic energy and potential energy of block at X is equal to the sum of the kinetic energy and potential energy of block at Z.
KX+UX=KZ+UZ
KX and KZ are zero because the block starts from rest and momentarily stops at the bottom.
UX=UZ
UZ is the result of compression of the spring due to the block.
MgH=21k[Δx]2
⇒H=2Mgk[Δx]2 ⇒H=2×10×10100×4 ⇒H=2 m
Now,
sin30∘H=(a+b)
Putting the values,
a=4−b (b is the change in length of spring)
⇒a=2 m
From the above diagram,
l=asin30∘
⇒l=1 m
Applying the law of conservation of energy at points X and Y.
KX+UX=KY+UY
KX is zero because the block starts from rest.
UX=KY+UY
⇒MgH=21MVY2+Mg(H−l)
⇒VY=2gl ⇒VY=20 ∴VY≈4.47 m/s
Therefore, the correct option is A.
Note: The potential energy of the block M at point Y is Mg(H−l). When the block is at rest kinetic energy becomes zero since the velocity of the body is zero. Also remember before touching the spring the block possesses both kinetic and potential energy since its motion does not cease on touching the spring.
