Question

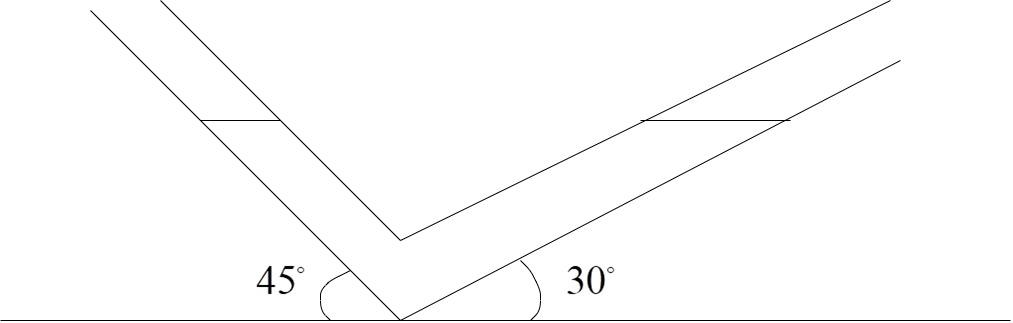
An ideal liquid is oscillating in a V tube as shown. If the total length of liquid column in the tube is $l$ then time period of oscillation is

A) $2\pi \sqrt {\dfrac{l}{{g\sqrt 2 }}}$
B) $2\pi \sqrt {\dfrac{l}{{g\sqrt 2 + 1}}}$
C) $2\pi \sqrt {\dfrac{l}{{g\sqrt 2 - 1}}}$
D) $2\pi \sqrt {\dfrac{l}{{g\sqrt 2 + 2}}}$

Answer 1

Whenever there is oscillation in the system, we need to understand the most basic equation/fact that the acceleration of the system is directly proportional to the displacement at any point in the system.

Formula used:
$a = - {\omega ^2}x$
where $\omega$ is the angular frequency of the system, which can be used to calculate the time period and the frequency. This is the way to approach this problem.

Complete step by step answer:
Consider the V-tube as shown below, with the limbs inclined at ${45^ \circ }$ and ${30^ \circ }$

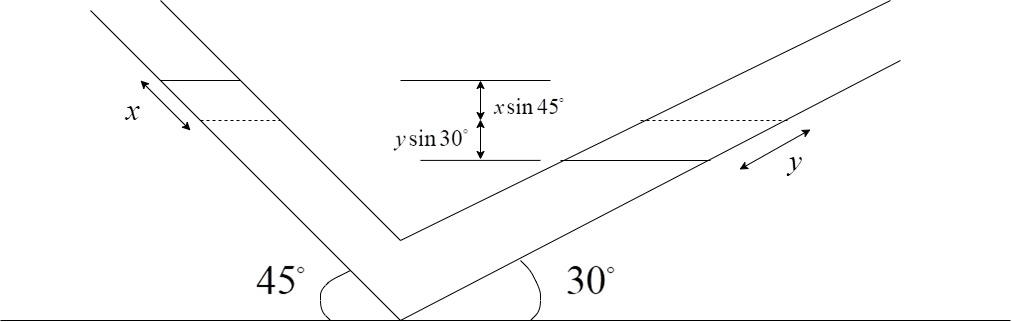
Here, the liquid undergoes a slight displacement $x$ in the left wing and because of that, there is a decrease of $y$ in the right wing as shown.
We can see in the image that the distances $x$ and $y$ are measured along the direction of the tube and their vertical distances are the sine components of the angles made the limb of the V-tube as shown.
The rise in the height of water in the left wing is equal to the dip in the height of water in the right wing.
This means that,
$x\sin 45 = y\sin 30$
$\dfrac{x}{{\sqrt 2 }} = \dfrac{y}{2}$
$\Rightarrow y = \sqrt 2 x$
The restoring force for the displacement in this case, will be the pressure force which is determined by the pressure difference between the topmost and the bottom-most level.
Pressure, $P = \rho gh$
where $\rho$ is the density and g is the acceleration due to gravity.
The height difference between the levels from the figure:
$h = x\sin 45 + y\sin 30$
$h = \dfrac{x}{{\sqrt 2 }} + \dfrac{y}{2}$

Substituting the value of y,
$h = \dfrac{x}{{\sqrt 2 }} + \dfrac{x}{{\sqrt 2 }}$
$\Rightarrow h = \sqrt 2 x$
Thus,
Pressure, $P = \sqrt 2 \rho gx$
Pressure is defined as the force per unit area, $P = \dfrac{F}{A}$
Also, force, $F = ma$
Substituting all the values, we have –
$\sqrt 2 \rho gx = \dfrac{{ma}}{A}$
The mass of the liquid, $m = V \times \rho = Al\rho$ where V is the volume of the liquid, A is the area of cross-section of the tube and $l$ is the total length of the liquid column.
Substituting, we get –
$\sqrt 2 \rho gx = \dfrac{{Al\rho a}}{A}$
$\Rightarrow al = \sqrt 2 gx$
$\Rightarrow a = \dfrac{{\sqrt 2 g}}{l}x$
Comparing this to the standard equation for oscillation, $a = {\omega ^2}x$ , we get –
${\omega ^2} = \dfrac{{g\sqrt 2 }}{l}$
The relationship between the angular frequency and the time period is given by –
$\omega = \dfrac{{2\pi }}{T}$
Substituting and rearranging,
$T = \dfrac{{2\pi }}{{\sqrt {\dfrac{{g\sqrt 2 }}{l}} }}$
$\Rightarrow T = 2\pi \sqrt {\dfrac{l}{{g\sqrt 2 }}}$

Hence, the correct option is Option A.

Note: Whenever you get any question on any oscillation system, the first thing to note is the basic relationship between the force and the displacement. From this, we can arrive at the value of the angular frequency and that can be used to obtain the frequency and time period.
This procedure can be easily implemented to solve any complex oscillation system given in any competitive exams.