Question
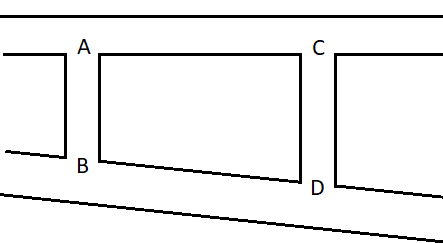
Question: An ideal liquid is flowing in 2 pipes AC and BD. One is inclined and the second is horizontal. Both ...
An ideal liquid is flowing in 2 pipes AC and BD. One is inclined and the second is horizontal. Both the pipes are connected by 2 vertical tubes. Assuming streamlines flow everywhere, if velocity of liquid at A, B and C are 2m/s, 4m/s and 4m/s respectively, what will be the velocity at D.
Solution
Hint
Here we can use Bernoulli's theorem to find the equation of the flow of water at the points A, B, C and D. Then we can write the equations as point A and C as equal and from there find the pressure difference between point A and C. Using that in the equations of point B and D we can find the answer.
In this solution we will be using the following equation,
⇒P+21ρv2+hρg=constant
where P is the pressure,
ρ is the density of the liquid
v is the velocity of the liquid
h is the height and g is the acceleration due to gravity.
Complete step by step answer
Let us consider the height between the points A and B is h1 and that between the points C and D is h2. According to Bernoulli's theorem, for steady, irrotational motion of a fluid, the addition of the pressure head, kinetic energy head and the gravitational head is constant.
Therefore we can write, P+21ρv2+hρg=constant
We consider the pressure at the point A, B, C and D PA, PB, PC and PD respectively and the velocities as, vA, vB, vC and vD .
Therefore, according to the figure, we can write the equation for the points A and C as,
⇒PA+21ρvA2+h1ρg=constant for the point A.
and PC+21ρvC2+h2ρg=constant for the point C.
We can equate them and hence get,
⇒PA+21ρvA2+h1ρg=PC+21ρvC2+h2ρg
We take the terms containing h1 and h2 to the RHS and get,
⇒PA+21ρvA2=PC+21ρvC2+(h2−h1)ρg
We can take the pressure terms and bring them to the LHS and take the rest terms to RHS and get
⇒PA−PC=21ρ(vC2−vA2)+(h2−h1)ρg
Similarly the Bernoulli’s equation for the points B and D are
⇒PB+21ρvB2=constant, as there is no height.
and PD+21ρvD2=constant
Equating these two we get,
⇒PB+21ρvB2=PD+21ρvD2
Now we can write the pressure at point B is equal to, PB=PA+h1ρg
and the pressure at the point D is equal to PD=PC+h2ρg
So substituting these in the equation we get,
⇒PA+h1ρg+21ρvB2=PC+h2ρg+21ρvD2
Now we bring the pressure terms to the LHS and take the other terms to the RHS and get,
⇒PA−PC=(h2−h1)ρg+21ρ(vD2−vB2)
Now in place of PA−PC we can substitute PA−PC=21ρ(vC2−vA2)+(h2−h1)ρg
Therefore, we get
⇒21ρ(vC2−vA2)+(h2−h1)ρg=(h2−h1)ρg+21ρ(vD2−vB2)
The term (h2−h1)ρg gets cancelled from both sides of the equation. Therefore we have,
⇒21ρ(vC2−vA2)=21ρ(vD2−vB2)
Further cancelling the 21ρ from both sides we get,
⇒vC2−vA2=vD2−vB2
Now keeping the velocity of water at the point D on one side and taking all the other terms to the other side we get,
⇒vD2=vC2−vA2+vB2
In the question we are given vA=2m/s, vB=4m/s and vC=4m/s
Therefore, substituting the values we get,
⇒vD2=(4)2−(2)2+(4)2
On doing the squares and adding, the value we get is,
⇒vD2=16−4+16=28
Therefore, taking square root on both sides,
⇒vD=28m/s
Hence the velocity of water at the point D is 28m/s .
Note
Bernoulli's theorem in fluid dynamics is a relation between the pressure, velocity and the elevation of the moving fluid where we consider the fluid to be incompressible, having negligible viscosity and in a steady irrotational flow. It can be derived from the law of conservation of energy, which states that in a steady flow, the sum of all forms of energy in a fluid along a streamline is the same at all points.
