Question

An ideal gas undergoes a thermodynamic process described by the equation: $PV^2 = C$, where C is a constant. The gas transitions from an initial state $(P_1, V_1, T_1)$ to a final state $(P_2, V_2, T_2)$. Which of the following statements is correct?

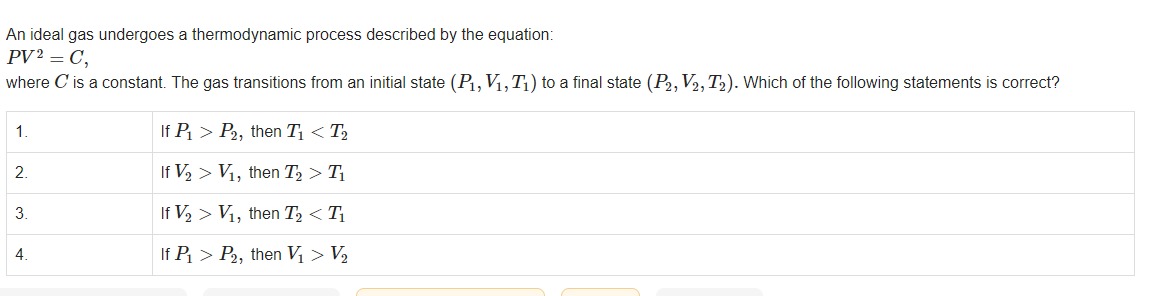
• A. If $P_1 > P_2$, then $T_1 < T_2$
• B. If $V_2 > V_1$, then $T_2 > T_1$
• C. If $V_2 > V_1$, then $T_2 < T_1$
• D. If $P_1 > P_2$, then $V_1 > V_2$

Answer 1

Answer: (C)

If $V_2 > V_1$, then $T_2 < T_1$

Answer 2

The ideal gas law is $PV = nRT$. The given process is $PV^2 = C$.

From these, we can express temperature $T$ as $T = \frac{PV}{nR}$.

1. Substituting $P = C/V^2$ into the expression for $T$: $T = \frac{(C/V^2)V}{nR} = \frac{C}{nR V}$. This shows $T \propto \frac{1}{V}$.

2. Substituting $V = \sqrt{C/P}$ into the expression for $T$: $T = \frac{P\sqrt{C/P}}{nR} = \frac{\sqrt{C}\sqrt{P}}{nR}$. This shows $T \propto \sqrt{P}$.

Option 3 states: If $V_2 > V_1$, then $T_2 < T_1$. This is consistent with the relationship $T \propto \frac{1}{V}$, as an increase in volume implies a decrease in temperature for this process.