Question

An ideal gas is trapped between the mercury column and the closed end of a narrow vertical tube containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure is equal to 76cm of Hg. The lengths of mercury column and trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column if the tube is tiled in the vertical plane with an of ${60^ \circ }$? Assume the temperature to be constant.

Answer 1

In this question we have to do the analysis of pressure at the bottom of the flask. Doing so in the two given conditions will give us the new length of air columns.

Complete step by step solution:

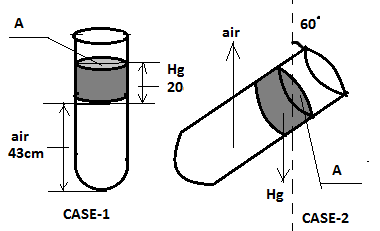
Case 1: Before tilting;
Let the pressure of trapped air be ${P_1}$
This will be the pressure at the air-mercury interface.
Also atmospheric pressure ( ${P_0}$ ) = 76 cm of Hg.
Now at point on the air-mercury interface the pressure will be;
${P_0} + {P_{Hg}} = {P_1}$
${P_1} = 76 + 20 = 96$ (Equation: 1)
Now since air is an ideal gas it will have uniform pressure throughout it. So the pressure at the bottom of the flask will be ${P_1} = 96$
Let the area of the tube be A
So applying gas law we get;
${P_1}V = nRT$
Now we all know, $V = Al$
And $l = 43cm$
Thus $\Rightarrow 96(A \times 43) = nRT$ (Equation: 2)
Now let us consider case 2 (after tilling);
The pressure at the air mercury interface ( ${P_2}$ ) is given by;
${P_2} = {P_0} + {P_{Hg}}\cos ({60^ \circ })$
Thus, $\Rightarrow {P_2} = 79 + \dfrac{{20}}{2} = 86$
Now applying gas law we get;
${P_2}V = nRT$
$\Rightarrow 86(Al') = nRT$ (Equation: 3) (here, $l'$ is the new length of air column)
From equation 2 and equation 3 we get;
$\Rightarrow 96 \times 43A = 86Al'$
$\therefore l' = \dfrac{{96 \times 43}}{{86}} = 48cm$

Therefore, the new length is 48 cm.

Note: The volume is changing and hence the area is constant.
If the lid will be closed the volume won’t change and hence the area will change.
The pressure balancing should be done carefully.