Question

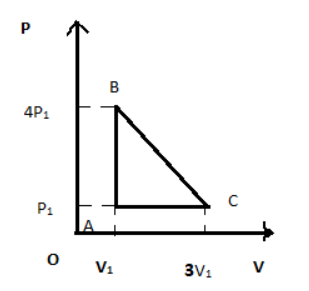
An ideal gas is taken around the cycle ABCA shown in P-V diagram. The network done by the gas during the cycle is equal to:

A. $12{P_1}{V_1}$
B. $6{P_1}{V_1}$
C. $3{P_1}{V_1}$
D. ${P_1}{V_1}$

Answer 1

As we know that the Ideal gas is perfectly elastic its rebound when it collides perfectly no losses are considered in ideal gas else this atom does not interact with each other and hence any change in energy is considered a change in temperature.
It can be distinguished in three-character absolute pressure (p), Volume (V) and Temperature (T). We can further provide this relationship of character as $PV = nRT$

Complete answer:
In the given above question we have to first consider ideal gas around the circular path as shown in figure ABCA,
We have to find out here the network done in the cycle
The cycle is equal to the work done,
So, Work done = Area under the curve
Hence work done = Area bounced (ABCA)

$$Area = \dfrac{1}{2} \times AC \times AB \\\ = \dfrac{1}{2} \times (3{V_1} - {V_1})(4{P_1} - {P_1}) \\\$$

So now equating in area of triangle formula we get,

$$Area = \dfrac{1}{2} \times AC \times AB \\\ = \dfrac{1}{2} \times (3{V_1} - {V_1})(4{P_1} - {P_1}) \\\$$

So, by solving above equation
$=\dfrac{1}{2} \times 2{V_1} \times 3{P_1}$
So, we get, $Area=3{P_1}{V_1}$
So, network done by the gas during the cycle is equal to $3{P_1}{V_1}$

**Hence the correct answer in option C

Additional Information:**
The net work completed by the gas in one cycle of a procedure with the aim of returning the gas to its primary condition is the area contained by the closed circuit in the PV diagram. If the circuit is traversed in a clockwise way the net effort is positive. But the loop is traversed in a counterclockwise way the net work is negative.

Note:
P-V diagram shows the change in volume and pressure in the system, it is actually used in thermodynamics. Writing the correct formula for each process is important as change in conditions will cause the formula to change.