Question
Question: An ideal gas is expanding such that $pT^2$ = constant. The coefficient of volume expansion of the ga...
An ideal gas is expanding such that pT2 = constant. The coefficient of volume expansion of the gas is
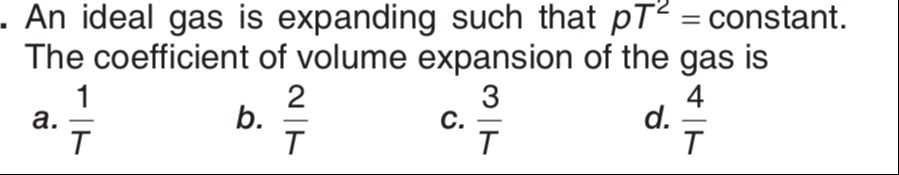
T1
T2
T3
T4
T3
Solution
The coefficient of volume expansion β is generally defined as β=V1(∂T∂V)p. This is the isobaric coefficient of volume expansion. However, for a process defined by a specific relation between thermodynamic variables, the coefficient of volume expansion is often interpreted as V1dTdV along the path of the process.
We are given that an ideal gas is expanding such that pT2=C, where C is a constant. The equation of state for an ideal gas is pV=nRT, where n is the number of moles and R is the ideal gas constant.
From the ideal gas equation, we can express pressure p as p=VnRT. Substitute this expression for p into the given process relation: (VnRT)T2=C VnRT3=C
Now, we can express the volume V as a function of temperature T for this process: V=CnRT3
To find the coefficient of volume expansion for this process, we need to calculate V1dTdV. First, let's find the derivative of V with respect to T: dTdV=dTd(CnRT3) Since n, R, and C are constants, we can take them out of the differentiation: dTdV=CnRdTd(T3) dTdV=CnR(3T2) dTdV=C3nRT2
Now, we can calculate the coefficient of volume expansion βprocess=V1dTdV: βprocess=(CnRT3)1(C3nRT2) βprocess=nRT3C×C3nRT2
Cancel out the common terms n, R, T2, and C: βprocess=T3
Thus, the coefficient of volume expansion of the gas for the given process pT2=constant is T3.
