Question

An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass M. The piston and cylinder have equal cross sectional area A. When the piston is in equilibrium, the volume of the gas is ${V_0}$ and its pressure is ${P_0}$​. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency.
A. $\dfrac{1}{{2\pi }}\dfrac{{{V_0}M\left( {{P_0} + \dfrac{{Mg}}{A}} \right)}}{{{A^2}\gamma }}$
B. $\dfrac{1}{{2\pi }}\sqrt {\dfrac{{{A^2}\gamma \left( {{P_0} + \dfrac{{Mg}}{A}} \right)}}{{M{V_0}}}}$
C. $\dfrac{1}{{2\pi }}\sqrt {\dfrac{{M{V_0}}}{{A\gamma \left( {{P_0} + \dfrac{{Mg}}{A}} \right)}}}$
D. $\dfrac{1}{{2\pi }}\dfrac{{A\gamma \left( {{P_0} + \dfrac{{Mg}}{A}} \right)}}{{{V_0}M}}$

Answer 1

In case of finding frequency or time period for SHM the first thing we should do is balance the forces as initially the system will be in equilibrium. Later provide very small displacement and then restoring force will act due to imbalance in forces and it tries to bring the system back to equilibrium condition. From this equation we can find out the time period and frequency and angular velocity.
Formula used:
${F_r} = - m{\omega ^2}x$
$\omega = 2\pi f$
$P{V^\gamma } = K$

Complete answer:
Initially the piston is in equilibrium condition. That means forces are balanced. Let P be the pressure acting of the gas. Same pressure will be acting on the piston and due to this gas pressure force will act upwards on the piston and will be balanced by weight. The diagram below represents the equilibrium situation.

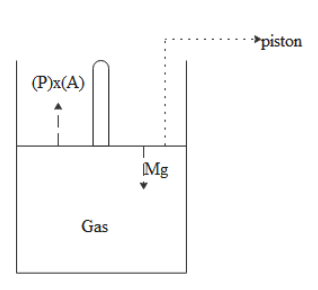
By balancing we get
$PA = Mg$
Where A is the area of the cross section of the piston and ‘g’ is the acceleration due to gravity and M is the mass of the piston.
Let us assume we move the piston by ‘x’ displacement. Then pressure will be increased by $dP$. Restoring force will be ${F_r} = - m{\omega ^2}x$
Then the force equation will be
\eqalign{ & (P + dP)A - Mg = - M{\omega ^2}x \cr & \Rightarrow (dP)A = - M{\omega ^2}x \cr}
It is given that the system is isolated which means the processes will be adiabatic as there will be no heat transfer with surroundings. Adiabatic equation will be
$P{V^\gamma } = K$
By differentiating this we will get
$dP = \dfrac{{ - \gamma P}}{V}dV$ … eq 1
Where $\gamma$ is the ratio of specific heats.
As ‘x’ amount of small displacement Is given the change in volume will be negative as volume decreases and volume change will be
$dV = - Ax$
By substituting above result in equation 1 we get
$dP = \dfrac{{ - \gamma P}}{V}dV$
$\Rightarrow dP = \dfrac{{\gamma P}}{V}Ax$
By substituting dP value in $(dP)A = - M{\omega ^2}x$ we get
$(dP)A = - M{\omega ^2}x$
\eqalign{ & \Rightarrow \dfrac{{\gamma P}}{V}{A^2}x = - M{\omega ^2}x \cr & \Rightarrow \omega = \sqrt {\dfrac{{\gamma P{A^2}}}{{{V_0}M}}} \cr}
We know pressure acting on gas = pressure acting on piston = P
$P = {P_0} + \dfrac{{Mg}}{A}$
$\Rightarrow \omega = 2\pi f$
By substituting the above results in $\omega = \sqrt {\dfrac{{\gamma P{A^2}}}{{{V_0}M}}}$ we get
$\Rightarrow f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{{A^2}\gamma \left( {{P_0} + \dfrac{{Mg}}{A}} \right)}}{{M{V_0}}}}$

Hence option B will be correct.

Note:
These all equations are valid only for the small displacements given. Even though the pressure of the gas given is some value, we should add the pressure created due to piston weight on the gas also to get the gas pressure and substitute it as pressure applied by gas on the piston in all the equations. That’s how we got $P = {P_0} + \dfrac{{Mg}}{A}$ rather than ${P_0}$.