Question

An ideal fluid of density $\rho$ is filled in a horizontally fixed syringe fitted with a piston. There is no friction between the piston and the inner surface of the syringe. The cross-section area of the syringe is $A$ . At one end of the syringe, an orifice of negligible cross-section area is made. When the piston is pushed into the syringe, the liquid comes out of the orifice and then following a parabolic path falls on the ground. With what speed the liquid strikes the ground? Neglect the air drag.
A. $\sqrt {\dfrac{{F + \rho ghA}}{{\rho A}}}$
B. $\sqrt {\dfrac{{F + 2\rho ghA}}{{\rho A}}}$
C. $\sqrt {\dfrac{{2F + \rho ghA}}{{\rho A}}}$
D. $\sqrt {\dfrac{{2(F + \rho ghA)}}{{\rho A}}}$

Answer 1

From the given data, first we need to calculate the velocity of the piston in the initial point and orifice point when it is pushed into the syringe. After that, we will find the net speed of the liquid that strikes the ground. The velocity of the piston is the change in displacement of the piston with respect to time.

Complete step by step answer:
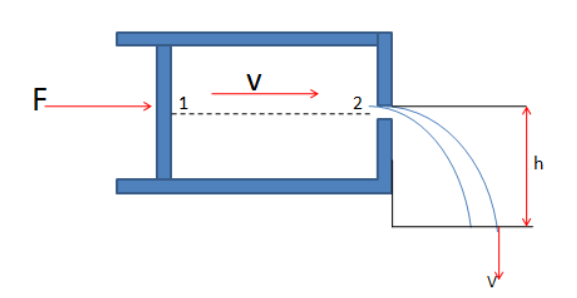
An ideal fluid of density $\rho$ is filled in a horizontally fixed syringe fitted with a piston.There is no friction between the inner surface of the syringe and the piston. $A$ is the cross-section area of the syringe. An orifice of negligible cross-section area is made at one end of the syringe. When the piston is pushed into the syringe, the liquid comes out of the orifice from point $1$ to point $2$ ; it is mentioned in the diagram, and then following a parabolic path falls on the ground.

When the piston is pushed into the syringe, pressure is created in that area. Where ${P_1}$ is the pressure at point $1$ and ${P_2}$ is the pressure at point $2$ . ${v_1}$ is the velocity at point $1$ and ${v_2}$ is the velocity at point $2$ . F is the force applied on the piston, h is the height of the parabolic path. We know that, $P = {P_1} = {P_2}$. And,
$\dfrac{F}{A} = \dfrac{1}{2}\rho {v_1}^2$.

${P_1} + \dfrac{1}{2}\rho {v_1}^2 + 0 = {P_2} + \dfrac{1}{2}\rho {v_2}^2 + 0$
$\Rightarrow P + \dfrac{F}{A} = P + \dfrac{1}{2}\rho {v_2}^2$
$\Rightarrow {v_2}^2 = \dfrac{{2F}}{{A\rho }}$
The velocity at point $2$,
{v_2} = \sqrt {\dfrac{{2F}}{{A\rho }}} $$$$$$ The velocity at point $1$ , {v_1}^2 = 2gh$$ \Rightarrow {v_1} = \sqrt {2gh} $The speed of the liquid strikes the ground,${v_{net}} = \sqrt {{v_2}^2 + {v_1}^2} $$\Rightarrow {v_{net}} = \sqrt {\dfrac{{2F}}{{A\rho }} + 2gh} $$\therefore {v_{net}} = \sqrt {\dfrac{{2\left( {F + \rho ghA} \right)}}{{\rho A}}} $$$$$$

Hence, option D is correct.

Note: The force exerted per unit area is called pressure. Volumetric flow is the rate of flow of the volume of liquid. The range is the horizontal distance that a body travels having some initial velocity the body can be on the ground initially and the body can also be at some height and can travel some distance.