Question

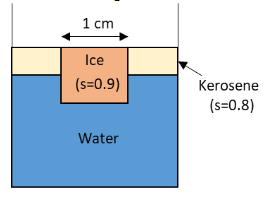
An ice cube of side 1cm is floating at the interface of kerosene and water in a beaker of base area $10\,{\text{c}}{{\text{m}}^2}$. The level of kerosene is just covering the top surface of the ice cube.
a. Find the depth of submergence in kerosene and that in the water.
b. Find the change in the total level of the liquid when the whole ice melts into water.

Answer 1

Use the formula for the upward buoyant force and using the law of floatation calculate the submergence of the ice cube in the kerosene and water. Then calculate the volume of the ice cube and its volume when it melts. Determine the rise in the water level when the ice cube melts and fall in the water level when the ice cube melts and calculate the net change in the level of the liquid.

Formulae used:
The Buoyant force ${F_B}$ on an object immersed in a liquid is
${F_B} = \rho Vg$ …… (1)
Here, $\rho$ is density of the liquid, $V$ is volume of the object immersed in the water and $g$ is acceleration due to gravity.
The density $\rho$ of an object is given by
$\rho = \dfrac{m}{V}$ …… (2)
Here, $m$ is the mass of the object and $V$ is the volume of the object.

Complete step by step solution:
We have given that the side of the ice cube is $1\,{\text{cm}}$.
$L = 1\,{\text{cm}}$
From the figure, the densities of kerosene and ice are $0.9{\rho _W}$ and $0.8{\rho _W}$ respectively.
${\rho _I} = 0.9{\rho _W}$
${\rho _K} = 0.8{\rho _W}$
Here, ${\rho _W}$ is the density of the water.

a. We know that the total height of the ice cube is equal to the height of ice cube in kerosene and in water.
$\Rightarrow {h_I} = {h_K} + {h_W}$
Here, ${h_I}$ is the height of the ice cube, ${h_K}$ is height of the ice cube in kerosene and ${h_W}$ is height of the ice cube in water.
According to the law of floatation, the weight of the ice cube is equal to the buoyant force acting on the ice block due to kerosene and water.
${W_I} = {\rho _K}Vg + {\rho _W}Vg$
$\Rightarrow {\rho _I}A{h_I}g = {\rho _K}A{h_K}g + {\rho _W}A{h_W}g$
$\Rightarrow {\rho _I}{h_I} = {\rho _K}{h_K} + {\rho _W}{h_W}$
Substitute $0.9{\rho _W}$ for ${\rho _I}$ and $0.8{\rho _W}$ for ${\rho _K}$ in the above equation.
$\Rightarrow 0.9{\rho _W}{h_I} = 0.8{\rho _W}{h_K} + {\rho _W}{h_W}$
$\Rightarrow 0.9{h_I} = 0.8{h_K} + {h_W}$
Substitute ${h_K} + {h_W}$ for ${h_I}$ in the above equation.
$\Rightarrow 0.9\left( {{h_K} + {h_W}} \right) = 0.8{h_K} + {h_W}$
$\Rightarrow 0.9{h_K} + 0.9{h_W} = 0.8{h_K} + {h_W}$
$\Rightarrow 0.9{h_K} - 0.8{h_K} = {h_W} - 0.9{h_W}$
$\Rightarrow 0.1{h_K} = 0.1{h_W}$
$\therefore {h_K} = {h_W}$
The total height of the ice cube is $1\,{\text{cm}}$. Since the height of the ice cube in water and in kerosene is the same.

The submergence of the ice cube in the kerosene and water is $0.5\,{\text{cm}}$.

b. The base area of the beaker is $10\,{\text{c}}{{\text{m}}^2}$.
$A' = 10\,{\text{c}}{{\text{m}}^2}$
When $1\,{\text{c}}{{\text{m}}^3}$ of the ice melts, the volume of the water formed is $0.9\,{\text{c}}{{\text{m}}^3}$.
The volume of the ice cube in the kerosene is $0.5\,{\text{c}}{{\text{m}}^3}$. After the volume of the ice in the kerosene is melted, the rise $\Delta {h_K}$ in liquid level is given by
$\Delta {h_K} = \dfrac{{0.5\,{\text{c}}{{\text{m}}^3}}}{{A'}}$
The volume of the ice cube in the water is given by
${V_W} = 0.9\,{\text{c}}{{\text{m}}^3} - 0.5\,{\text{c}}{{\text{m}}^3}$
$\Rightarrow {V_W} = 0.4\,{\text{c}}{{\text{m}}^3}$
Hence, the rise in the level of the water when the ice is melted is given by
$\Delta {h_W} = \dfrac{{0.4\,{\text{c}}{{\text{m}}^3}}}{{A'}}$
Hence, the net fall in the level is
$\Delta h = \Delta {h_K} - \Delta {h_W}$
$\Rightarrow \Delta h = \dfrac{{0.5\,{\text{c}}{{\text{m}}^3}}}{{A'}} - \dfrac{{0.4\,{\text{c}}{{\text{m}}^3}}}{{A'}}$
$\Rightarrow \Delta h = \dfrac{{0.1\,{\text{c}}{{\text{m}}^3}}}{{A'}}$
$\Rightarrow \Delta h = \dfrac{{0.1\,{\text{c}}{{\text{m}}^3}}}{{10\,{\text{c}}{{\text{m}}^2}}}$
$\Rightarrow \Delta h = 0.01\,{\text{cm}}$
$\therefore \Delta h = 0.1\,{\text{mm}}$

Hence, the change in the whole level of the liquid when the ice cube melts is $0.1\,{\text{mm}}$.

Note: The students should keep in mind that the net change in the level of the liquid when the ice cube melts is negative because the fall in the level of the liquid as compared to the ride in level of the liquid when the ice cube melts is high. As we have only asked to calculate the change in the liquid level, we have not mentioned the sign of the change in level of the liquid.