Question

An ice cube is kept on inclined Plane of angle $30{}^\circ$ coefficient of kinetic friction between block incline plane is $\dfrac{1}{\sqrt{3}}$ what is acceleration of block
A. Zero
B. $2m/{{s}^{2}}$
C. $1.5m/{{s}^{2}}$
D. $5m/{{s}^{2}}$

Answer 1

As ice cube is kept on an inclined plane so it is needed to find out the components of weight (mg) of ice cube. Also friction forces act opposite to the motion of objects.

Complete answer:
A diagram can be illustrated as follows:

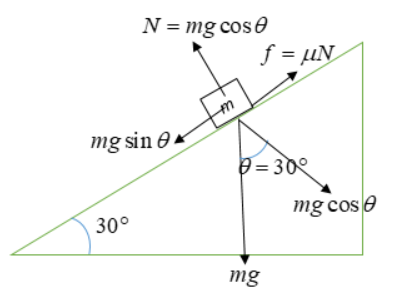
As given inclination of Plane is $\theta =30{}^\circ$
Coefficient of kinetic Friction between the block and incline plane $\left( \mu \right)=\dfrac{1}{\sqrt{3}}$
Let the mass of the ice cube is M.
Which is moving with acceleration a
As the weight of the ice piece acts downwards towards the center of earth which is mg.
Component of mg along plane $=mg\sin \theta$
Component of mg perpendicular to plane $=mg\cos \theta$
As the ice cube moves downwards on the incline plane, friction force (f) will act opposite to the motion of the ice cube.
As we know $f=\mu N\text{ }\left( 1 \right)$b
Here N is the normal between plane surface and ice cube.
By the above diagram
$N=Mg\cos \theta \text{ }\left( 2 \right)$
Also $Mg\sin \theta -f=ma\text{ }\left( 3 \right)$
By substituting values from equation 1 and 2 to equation 3
$\Rightarrow Mg\sin \theta -\mu mg\cos \theta =ma$
$\Rightarrow a=g\sin \theta -\mu g\cos \theta$
$\Rightarrow a=10\times \sin 30{}^\circ -\dfrac{1}{\sqrt{3}}\times 10\times \cos 30\text{ }\left[ g\approx 10m/{{s}^{2}} \right]$
$\Rightarrow a=10\times \dfrac{1}{2}-\dfrac{1}{\sqrt{3}}\times 10\times \dfrac{\sqrt{3}}{2}$
$\Rightarrow a=10\times \dfrac{1}{2}-10\times \dfrac{1}{2}$
$\Rightarrow a=5-5=0$
So, here we can say friction (f) is enough to balance $mg\sin \theta$

Hence, the correct choice is option A zero.

Note:
Friction Force between two contacting surfaces as an ice cube and plane will act in the opposite direction of motion. As the ice cube will move downwards on the incline plane so frictional Force acts upwards.