Question
Question: An extensible string is wound over a rough pulley of mass \({M_1}\) and radius \(R\) and a cylinder ...
An extensible string is wound over a rough pulley of mass M1 and radius R and a cylinder of mass M2 and radius R such that as the cylinders roll down, the string unwound over the pulley as well the cylinder. Find the acceleration of cylinder M2.
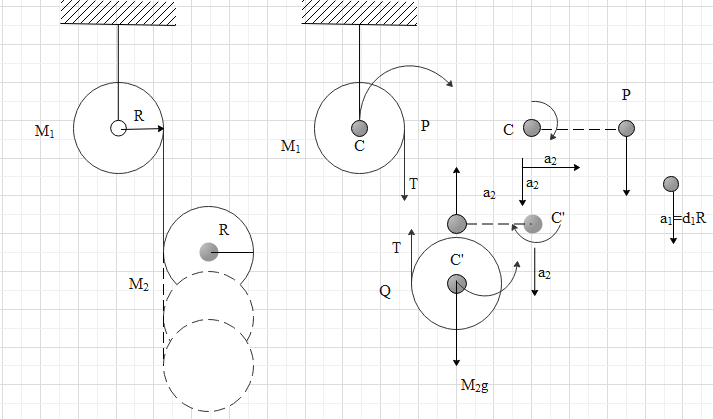
Solution
From the given information we can find that the pulley has only rotational motion but the cylinder will have both rotational and translational motion.
Torque is a product of the moment of inertia and angular acceleration.
τ=Iα
Where I is the moment of inertia and α is the angular acceleration.
Torque can also be found out by multiplying the force with the perpendicular distance.
τ=F×R.
Here the force acting is the tension T in the string and the perpendicular distance is R
Using the above two-equation, we can find the angular acceleration of both pulley and cylinder.
The linear acceleration of the cylinder can be found by writing the equation of motion for the cylinder.
The acceleration of the point P and Q will be the same since both are connected with the same string.
Using all this information, we can write equations and solve them for finding the acceleration of M2.
Complete step by step answer:
Given the mass of the pulley is M1
The radius of the pulley is R.
The mass of the cylinder is M2.
The radius of the cylinder is R.
Now the pulley has only angular acceleration let this be denoted as α1
This cylinder has both angular acceleration and linear acceleration.
Let the linear acceleration of the cylinder be denoted as a2 and the angular acceleration be denoted as α2.
Now let us derive the equation for angular acceleration for the pulley
Let the torque acting on the pulley be τ.
We know that torque is a product of moment of inertia and angular acceleration.
τ=Iα
Since pulley is disc shaped the moment of inertia of the pulley is
I1=21M1R2
Therefore,
τ=21M1R2×α1 ……………………..(1)
Torque can also be found out by multiplying the force with the perpendicular distance.
τ=F×R …………………………………………….(2)
Here the force acting is the tension T in the string and the perpendicular distance is R
On substituting we get
τ=T×R ………………………………………………..(3)
Now let us equate equations 1 and 3
21M1R2×α1=T×R
⇒α1=M1R2T
This is the angular acceleration in the pulley.
Now let us find the angular acceleration in the cylinder. Moment of inertia of the cylinder is
I2=21M2R2
The torque can be written as
τ=I2α2
τ=21M2R2×α2 ………………………...(4)
The force acting here is tension. And perpendicular distance is R
Therefore, using equation 3
τ=T×R …………………….(5)
Equating equations 4 and 5
21M2R2×α2=T×R
⇒α2=M2R2T
This is the angular acceleration of the cylinder.
In order to find the linear acceleration of the cylinder let us write the equation of motion for this cylinder.
The net force acting on the cylinder will be mass times acceleration
F=M2a2
The forces acting on the cylinder are force due to gravity M2g and tension T.
Therefor net force can be written as
M2a2=M2g−T
⇒T=M2(g−a2) …………………………………..(6)
Let us denote of the acceleration at point P as ap
Acceleration will be the product of angular acceleration and the perpendicular distance.
a=α×R
Therefore
At P, aP=α1R
Let the acceleration of point Q be aQ
This will be the net acceleration due to translation and rotation.
Thus,
aQ=a2−α2R
The acceleration of the point P and Q will be the same since both are connected with the same string.
Thus
aP=aQ
That is,
α1R=a2−α2R
⇒a2=α1R+α2R
Substitute the value of α1 and α2 in this equation.
a2=M1R2TR+M2R2TR
⇒a2=M1M22T(M1+M2)
Substitute the value of tension from equation 6
a2=M1M22M2(g−a2)(M1+M2)
⇒a2=M12g(M1+M2)−M12a2(M1+M2)
⇒M1a2=2g(M1+M2)−2a2(M1+M2)
∴a2=3M1+2M22g(M1+M2). This is the acceleration of cylinder M2.
Note:
Hear the pulley has only rotational motion. But the cylinder has both rotational and translational motion. The cylinder is moving downwards with rotation. Whereas the pulley is rotating at the given place itself it does not have a translational motion.
The points P and Q will have the same acceleration because they are connected by the same string. That is why we were able to equate the values of the net acceleration of P and Q.
