Question

An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground is $85{\text{ m}}$ and height of the cylindrical part is $50{\text{ m}}$. If the diameter of the base is ${\text{168 m}}$, find the quantity of the canvas required to make the tent. Allow $20\%$ extra for fold and far stitching. Give your answer to the nearest ${m^2}$.
A. $504053.012$
B. $50553.702$
C. $40423.712$
D. $50423.712$

Answer 1

In this question we will first draw a rough figure according to the information given in the question. In the question it is asked to find the quantity of the canvas required to make the tent and this is equal to the lateral surface area of the cylinder plus the lateral surface area of the cone. Also, we will add $20{\text{ }}{{\text{m}}^2}$ for fold and far stitching.

Complete step by step answer:

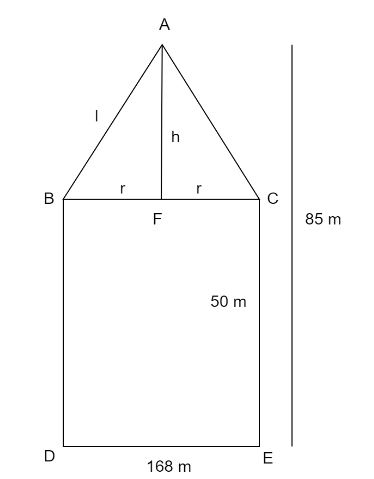
In the figure ABC is the conical part and DECB is the cylindrical part.
Total height of tent $= 85{\text{ m}}$
Height of cylindrical part $= 50{\text{ m}}$
height of conical part, $h = \left( {85 - 50} \right){\text{ m}}$
$\Rightarrow h = 35{\text{ m}}$
Now we have;
$BC = DE = 168{\text{ m}}$
Both are the diameter of the cylinder.
Also, we have
$r = BF = \dfrac{{BC}}{2}$

Putting the value of $BC$, we get;
$\Rightarrow r = \dfrac{{168{\text{ m}}}}{2}$
$\Rightarrow r = 84{\text{ m}}$
Now in triangle ABF, by Pythagoras theorem we have;
$A{B^2} = A{F^2} + B{F^2}$
Putting the value of sides, we have;
$\Rightarrow {l^2} = {h^2} + {r^2}$
Putting the values, we get;
$\Rightarrow {l^2} = \left( {{{35}^2} + {{84}^2}} \right){\text{ }}{{\text{m}}^2}$
$\Rightarrow {l^2} = 8281{\text{ }}{{\text{m}}^2}$

Taking square root of both sides we have;
$\Rightarrow l = \sqrt {8281} {\text{ m}}$
$\Rightarrow l = 91{\text{ m}}$
Now we know;
Lateral surface area of cylinder $= 2\pi \times {\text{ radius }} \times {\text{ height}}$
From the figure we have;
Lateral surface area of cylinder $= 2\pi \times BF \times CE$
Putting the values, we get;
Lateral surface area of cylinder $= 2\pi \times 84 \times 50{\text{ }}{{\text{m}}^2}$
Lateral surface area of cylinder $= 26,389.378{\text{ }}{{\text{m}}^2}$

Also, we have;
Lateral surface area of cone $= \pi rl$
Putting the values, we get;
Lateral surface area of cone $= \pi \times 84 \times 91{\text{ }}{{\text{m}}^2}$
$= 24,014.334{\text{ }}{{\text{m}}^2}$
Now,
Area of canvas required $=$ lateral surface area of cylinder $+$ lateral surface of cone + extra $20{\text{ }}{{\text{m}}^2}$
$\text{area of canvas required} = \left( {26389.378 + 24014.334 + 20} \right){\text{ }}{{\text{m}}^2}$
$\therefore \text{area of canvas required} = 50,423.712{\text{ }}{{\text{m}}^2}$

Therefore, the correct option is D.

Note: One important point to note here is that we have to cover only the outer curved surfaces of the tent and not the base of the tent. So, we will find the curved or lateral surface area and not the total surface area because in the total surface area base area will also be included. Another point to keep in mind is that the unit of area is meter square and we have to put it in our answer.