Question

An excited $H{e^ + }$ ion emits two photons in succession, with wavelengths 108.5 nm and 30.4 nm, in making a transition to ground state. The quantum number n, corresponding to its initial excited state is (for photon of wavelength $\lambda$, energy $E = \dfrac{{1240}}{{\lambda ({\text{in nm}})}}eV$)
A. n = 5
B. n = 4
C. n = 6
D. n = 7

Answer 1

The total energy emitted by the two de-excitations is equal to the sum of the energy of the two de-excitations and the Bohr model gives expression for total energy emitted when a hydrogen-like atom undergoes de-excitation from a higher energy state to lower energy state. By equating this formula and the sum of the given energies, we can find out the required value of n for the excited state.

Formula used:
According to Bohr model, the expression for total energy emitted when a hydrogen-like atom undergoes de-excitation from a higher energy state to lower energy state is given by the following formula.
$E = 13.6{Z^2}\left[ {\dfrac{1}{{n_1^2}} - \dfrac{1}{{n_2^2}}} \right]eV$
The energy is given in terms of the wavelength of a light by the following expression.
$E = \dfrac{{hc}}{\lambda }$

Complete step by step answer:
We are given an excited $H{e^ + }$ ion which is a hydrogen-like atom. It emits two photons in succession while making a transition to the ground state from the excited state. The two wavelengths emitted are given as
${\lambda _1} = 108.5nm \\\ {\lambda _2} = 30.4nm \\\$
The following diagram shows the energy levels for the given atom where the de-excitation takes from an energy level n to the ground state n = 1

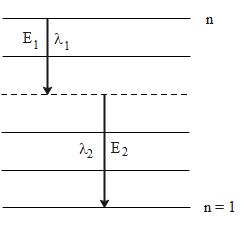
The energy emitted by a hydrogen-like atom in a single de-excitation from an excited state ${n_2}$ to a lower energy state ${n_1}$ is given by the following formula.
$E = 13.6{Z^2}\left[ {\dfrac{1}{{n_1^2}} - \dfrac{1}{{n_2^2}}} \right]eV$
Now for the given atom, Z = 2 and the total energy emitted by the two de-excitations is equal to the sum of the energy of the two de-excitations. Therefore, we have
$E = {E_1} + {E_2} \\\ \Rightarrow 13.6{Z^2}\left[ {\dfrac{1}{{{1^2}}} - \dfrac{1}{{{n^2}}}} \right] = \dfrac{{hc}}{{{\lambda _1}}} + \dfrac{{hc}}{{{\lambda _2}}} \\\ \Rightarrow 13.6 \times {\left( 2 \right)^2}\left[ {\dfrac{1}{{{1^2}}} - \dfrac{1}{{{n^2}}}} \right] = \dfrac{{1240eV/nm}}{{108.5nm}} + \dfrac{{1240eV/nm}}{{30.4nm}} = 11.43 + 40.79 = 52.22 \\\ \Rightarrow 1 - \dfrac{1}{{{n^2}}} = \dfrac{{52.22}}{{54.4}} \\\ \Rightarrow \dfrac{1}{{{n^2}}} = 1 - \dfrac{{52.22}}{{54.4}} = \dfrac{{2.18}}{{54.4}} \\\ \Rightarrow {n^2} = \dfrac{{54.4}}{{2.18}} = 25 \\\ \therefore n = 5 \\\$
This is the required value of n for the excited state. Hence, the de-excitation takes from n = 5 state, i.e. the fourth excited state,
So, the correct answer is option A.

Note:
Hydrogen-like atoms are those which have the same electronic configuration as that of a neutral hydrogen atom. The neutral helium atom is not hydrogen-like but if we remove one electron from it then we get the same electronic configuration as hydrogen. Similarly, other hydrogen-like atoms are $L{i^{2 + }}$, $B{e^{3 + }}$, etc.