Question
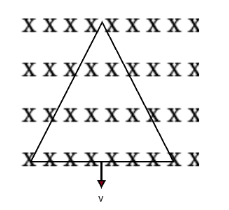
Question: An equilateral triangular loop ADC having some resistance is pulled with a constant velocity \( v \)...
An equilateral triangular loop ADC having some resistance is pulled with a constant velocity v out of a uniform magnetic field directed into the paper. At time t=0 side DC of the loop is at the edge of the magnetic field. The induced current versus time graph will be as
(A) 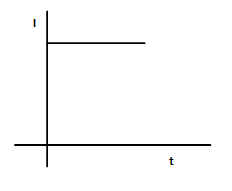
(B) 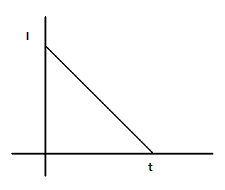
(C) 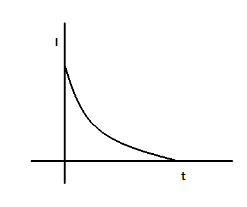
(D) 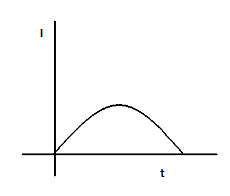
Solution
Hint : The potential difference induced in conductor is directly proportional to its length. Since, the triangular loop is being moved downward at a constant velocity the length within the magnetic field decreases uniformly.
Formula used: In this solution we will be using the following formula;
V=Blv , where V is the emf or potential difference induced in a conductor, B is the strength of the magnetic field or the magnetic flux density, l is the length of the conductor in the magnetic field, v is the velocity of the conductor in the magnetic field.
Complete step by step answer
Generally, emf will be induced on a conductor moving with a particular magnetic field even while the conductor is completely in the magnetic field. In our question above, the conductor uniformly moves out of the magnetic field gradually until it is completely out. To determine the voltage with time, we recall the formula for voltage induced in a conductor. This is given as
V=Blv , where V is the emf or potential difference induced in a conductor, B is the strength of the magnetic field or the magnetic flux density, l is the length of the conductor in the magnetic field, v is the velocity of the conductor in the magnetic field.
We see that in our triangle, the length in the field varies with time. Since
l=vt then
V=B(−vt)v=−Bv2t
Then the current is
I=B(−vt)v=−RBv2t (since V=IR )
As seen, the current varies linearly with time with a negative slope.
Hence, the correct option is B.
Note
In actuality, this is a simplified version of just to get the general relationship between the current and time. It can be proven that really, the voltage is given as
V=(h−bBv2t+2Bbv) . Where b and h are the length of one side of the equilateral triangle and the height respectively. This shows the negative slope and the intercept at the y-axis.
