Question

An equilateral triangular loop $ABC$ having some resistance is pulled with a constant velocity $v$ out of a uniform magnetic field directed into the paper (figure). At time $t=0$, side $BC$ of the loop is at the edge of the magnetic field. The induced current $i$ versus time $t$ graph will be as

(A).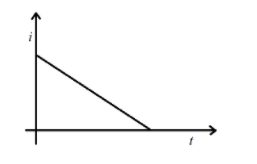
(B).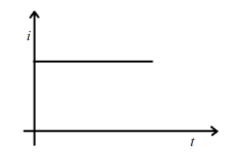

(C).

(D).

Answer 1

Hint: We can find the relation between induced current and the time by calculating the electromotive force generated in the loop. As the loop is moving with the constant velocity, we will find how the induced current is affected with the time.

Formula used:
Induced emf $=Blv$

Complete step by step answer:
Electromotive force is the electrical action produced by a non-electrical source. Devices provide an emf by converting other forms of energy into electrical energy, such as batteries and generators. Electromotive force, emf, is the energy generated per unit electric charge which is imparted by an energy source. Energy gets transformed from one form to another in a generator or battery as the device works on the electric charge being transferred within itself.
One of the major differences between Voltage and EMF is that EMF is the energy supplied to the charge while Voltage is the energy required to move the unit charge from one point to another.
An electromotive force is said to be induced when the flux linking with a conductor or coil changes. This change in flux can be obtained in two different ways; that is statically or by dynamically induced emf.
There can be three ways to induce emf in a loop of wire
Changing the magnetic field
Changing the area of the loop
Changing the angle between the magnetic field and the loop
In the above question, as the triangular loop will move with some velocity, the area associated with the magnetic field will keep on changing, resulting in the change of magnetic flux through the loop and generation of induced Electromotive force.
After $t=0$, as the triangular loop is pulled down, only the top two edges would remain in the field. The effective length of the top two edges inside the magnetic field keeps on increasing with time at a constant rate as the velocity of the loop is constant.
Therefore,
Induced emf $=Blv$
Where,
$B$ is the magnetic field
$l$ is the length of the triangle
$v$ is the velocity of the length of the length of the triangle
Curve obtained will be a straight line with a constant rate negative slope as the effective length $l$ keep on decreasing at a constant rate.
After the whole loop is outside the magnetic field, no more emf exits in the loop.
Hence, the correct option is B.

Note: Students should keep in mind that electromotive force is only induced in a loop or a coil or any conductor if magnetic flux associated with the conductor changes. And for varying the magnetic flux through a conductor we can change the value of the magnetic field; change the area of the loop, or change the angle between the magnetic field and the loop. In the above question the area of the loop inside the field was changing as the loop was moving with constant velocity.