Question
Question: An equilateral triangle wire frame of side L having 3 point charges at its vertices is kept in x-y p...
An equilateral triangle wire frame of side L having 3 point charges at its vertices is kept in x-y plane as shown. Components of the electric field due to the configuration in z-direction at (0, 0, L) is (origin is centroid of triangle).
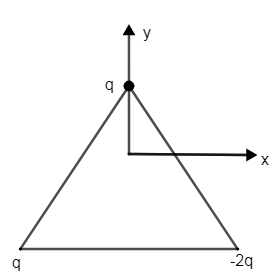
Solution
An equilateral triangle is the one in which all sides are equal. Firstly, calculate the distance of vertices of triangle from the centroid of the equilateral triangle then, find the components of the electric field in the z-direction at (0, 0, L) point.
Complete answer:
We know that an equilateral triangle is a triangle whose all three sides are of the same length. The sides of an equilateral triangle are congruent. The three angles are also congruent.to each other and are each 60o.

Now form the above figure, in ΔBED
