Solveeit Logo
Login

Question

Question: An equilateral triangle SAB is inscribed in the parabola \({y^2} = 4ax\) having its focus at S. If c...

An equilateral triangle SAB is inscribed in the parabola y2=4ax{y^2} = 4ax having its focus at S. If chord AB lies towards the left of S, then side length of the triangle is
A. 2a(2−3)2a\left( {2 - \sqrt 3 } \right)
B. 4a(2−3)4a\left( {2 - \sqrt 3 } \right)
C. a(2−3)a\left( {2 - \sqrt 3 } \right)
D. 8a(2−3)8a\left( {2 - \sqrt 3 } \right)

Explanation

Solution

Hint: To find the length of the triangle, begin by considering two points, using these two points find out the slope of AS using the formula of slope and find the value of t1{t_1}.

Complete step-by-step answer:


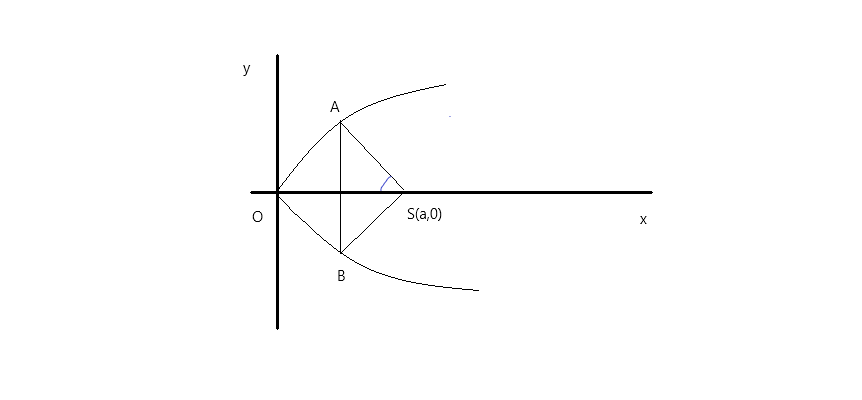
Let A(at12,2at1),B(at12,−2at1)A\left( {a{t_1}^2,2a{t_1}} \right),B\left( {a{t_1}^2, - 2a{t_1}} \right)

It is given that ∠ASO=π6\angle ASO = \dfrac{\pi }{6}, therefore the slope of AS will be,
mAS=tan⁡(5π6){m_{AS}} = \tan \left( {\dfrac{{5\pi }}{6}} \right)

On using the formula to find slope which is, m=y2−y1x2−x1m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}, we get,
⇒2at1at12−a=−13\Rightarrow \dfrac{{2a{t_1}}}{{a{t_1}^2 - a}} = - \dfrac{1}{{\sqrt 3 }}
⇒t12+23t1−1=0\Rightarrow {t_1}^2 + 2\sqrt 3 {t_1} - 1 = 0
⇒t12=−3±2\Rightarrow {t_1}^2 = - \sqrt 3 \pm 2

Clearly, t1=−3−2{t_1} = - \sqrt 3 - 2 is rejected.

Thus, t1=(2−3).{t_1} = \left( {2 - \sqrt 3 } \right).

Hence, AB=4at1=4a(2−3)AB = 4a{t_1} = 4a\left( {2 - \sqrt 3 } \right)

Option B is the correct answer.

Note: We started by assuming two points and then calculated the value of t1{t_1}using the formula of slope of AS. In this question, we rejected the negative value of t1{t_1}as it would not have matched with the given options.