Question

An equilateral triangle of side $9$ cm is inscribed in a circle. Find the radius of the circle.

Answer 1

First use the property of the equilateral triangle after constructing an altitude from the vertex D on the side BC. After that use the property of the subtended angle by an arc to get the desired result.

Complete step by step solution:
We have given an equilateral triangle of side $9$ cm inscribed in a circle.
The goal is to find the radius of the circle.

Now, draw a figure in which an equilateral triangle of side $9$ cm is inscribed in a circle. Then the figure is given as:

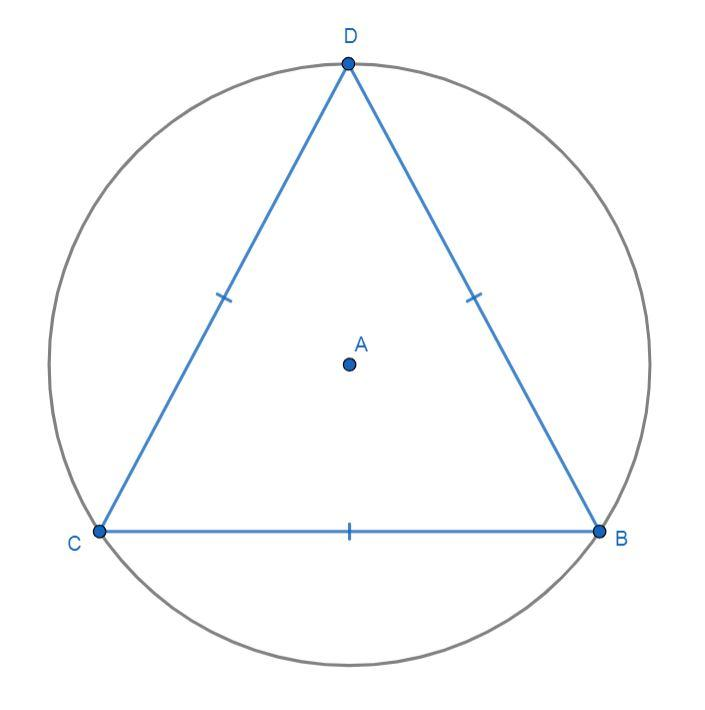
In the above figure, $BCD$ is an equilateral triangle which is inscribed in a circle whose center is $A$.

Since ABC is an equilateral triangle, then the altitude from its vertex to the corresponding side is the perpendicular bisector of the side even if it passes through the circumcenter of the triangle.

Now, for starting the problem we have made some construction. So, draw an altitude from the vertex $D$ on the side $BC$ at the point $O$, then the above figure becomes:

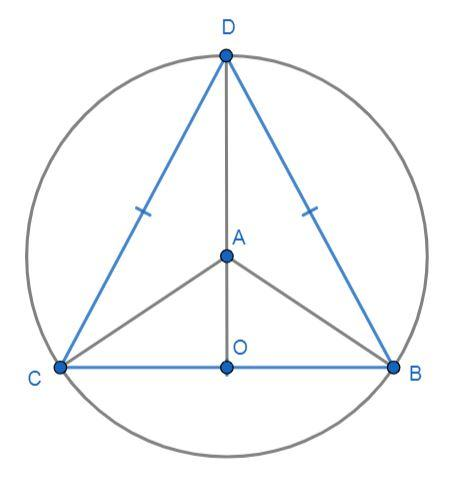
Now, take a look on the triangles $AOC$ and $AOB$,
$OC = OB$(D is the mid-point of BC)
$AB = AC$(Radius of the circle)
$AO = AO$(Common side of the triangle)

Therefore, using the $SSS$ rule of the congruency, we can say that the triangles $AOC$ and $AOB$ are congruent. That is
$\Delta AOC \cong \Delta AOB$
Then we have,
$\angle CAO = \angle BAO$

We know that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle. Then we can write,
$\angle CAB = 2\angle CDB$
As $\Delta BCD$ is an equilateral triangle, then each of its angles has a measure of $60^\circ$, thus
$\angle CDB = 60^\circ$
Using it we have,
$\angle CAB = 2 \times 60^\circ = 120^\circ$

Now, we can easily, break the angle $\angle CAB$ in the sum of two angles as:
$\angle CAB = \angle CAO + \angle BAO$
As we have$\angle CAO = \angle BAO$, then
$\angle CAB = \angle CAO + \angle CAO$
$\angle CAB = 2\angle CAO$
$\angle CAO = \dfrac{1}{2}\left( {\angle CAB} \right)$
Substitute the value $\angle CAB = 120^\circ$ into the equation:
$\angle CAO = \dfrac{1}{2}\left( {120^\circ } \right)$
$\angle CAO = 60^\circ$
As the altitude from the vertex D on the side, bisect the side BC, then
$CO = \dfrac{1}{2}\left( {CB} \right)$
Substitute the length of a side, $BC = 9$ into the equation:
$CO = \dfrac{1}{2}\left( 9 \right) = \dfrac{9}{2}$
Now, in the triangle CAO, we have
$\angle CAO = 60^\circ$and$CO = \dfrac{9}{2}$
Now, apply the trigonometric ratio in the triangle CAO, we have
$\sin A = \dfrac{{CO}}{{CA}}$
Substitute the values:
$\sin 60^\circ = \dfrac{{\dfrac{9}{2}}}{{CA}}$
$\Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{9}{{2CA}}$
Solve the equation for $CA$,
$CA = \dfrac{9}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }}$
$\Rightarrow CA = 3\sqrt 3$cm

Therefore, the radius of the circle is $3\sqrt 3$cm.

Note: The altitude drawn from the vertex on the side is perpendicular to the side and bisect it and also the altitude passes through the circumcenter of the triangle.