Question

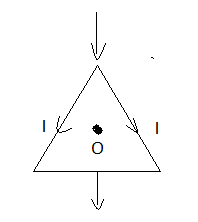
An equilateral triangle is made by uniform wires AB, BC, CA. A current I enters at A and leaves from the midpoint of BC. If the lengths of each side of the triangle is L, the magnetic field B at the centroid O of the triangle is
A. $\dfrac{{{\mu }_{\circ }}}{4\pi }\left( \dfrac{4I}{L} \right)$
B. $\dfrac{{{\mu }_{\circ }}}{2\pi }\left( \dfrac{4I}{L} \right)$
C. $\dfrac{{{\mu }_{\circ }}}{2\pi }\left( \dfrac{2I}{L} \right)$
D. Zero

Answer 1

This question can be solved by the principles of magnetic field in a loop and we will see Fleming's left hand rule to identify direction of magnetic field or induced current. By the help of Fleming’s left hand rule we will see about the direction of the magnetic field and how it cancels out the opposite field in that area.

Complete Step by step solution:
Question states that the triangle is equilateral so it's symmetric about midpoint or we can say can be cut in two equal halves.

So, the current flows in left and right parts of the given triangle will be equal and we can say that magnetic field due to both parts at point O will be equal and opposite to each other (By fleming's left hand rule) , so the overall magnetic field due to both parts will be zero as they will cancel out each other so the net magnetic field at O is zero.
${{\vec{B}}_{1}}+{{\vec{B}}_{2}}=0$
${{\vec{B}}_{1}}$(Magnetic field due to left part) and ${{\vec{B}}_{2}}$(Magnetic field due to right part)

So option D is correct.

Additional information:
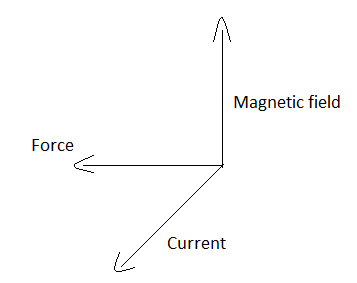
Fleming's Left hand rule finds the direction of magnetic force acting on a charge particle and we know that current and magnetic field will be there and perpendicular to each other so left hand rule is given by below diagram,

Note:
When a charge is moving in a magnetic field it experiences a perpendicular force to the direction of its velocity as well as to the magnetic field. While applying the left hand rule make sure all three fingers are perpendicular to each other to find the direction of inward or outward magnetic field.