Question

An equilateral triangle is inscribed in the parabola ${y^2} = 8x$, with one of its vertices is the vertex of the parabola. Then, the length of the side of that triangle is:
A. $24\sqrt 3$
B. $16\sqrt 3$
C. $8\sqrt 3$
D. $4\sqrt 3$

Answer 1

Construct a figure of an equilateral triangle which is in the parabola. With ${y^2} = 8x$ we will find the vertex of the parabola. As the equilateral triangle is inscribed in the parabola, so we can get the value of the angle at which the axis of the parabola bisects the angle. From the figure we can see that the side of the triangle intersects the parabola at $\left( {2{t^2},4t} \right)$, we can find the value of $t$ and substitute in the point. Thus, we will find the length of the side.

Complete step by step answer:

We will start by constructing a figure of an equilateral triangle that is inscribed in the parabola.
Here, we will compare the given parabola ${y^2} = 8x$, with ${y^2} = 4ax$ and find the value of $a$.
Thus, the value of $a$ is $a = 2$.
Now, we can find the coordinates of the triangle by substituting the value of $a$.
Thus, the figure is as follows:

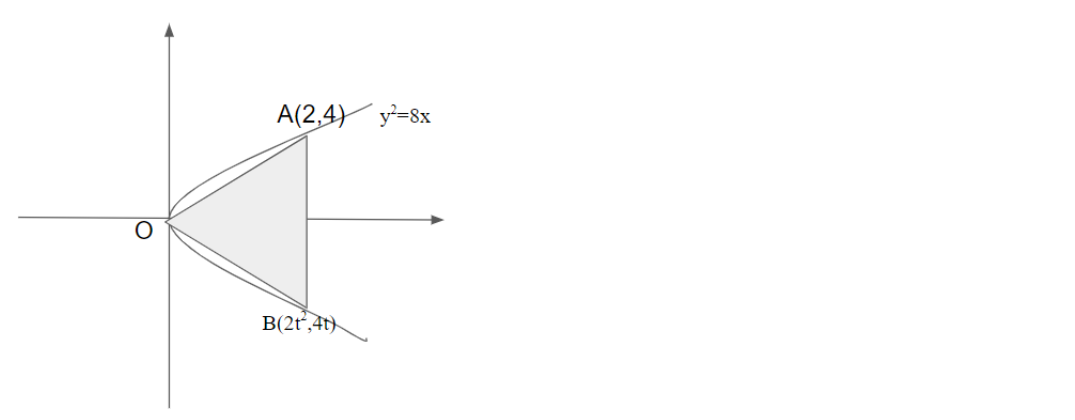
From the figure, we can see the vertex of the parabola is $\left( {0,0} \right)$.
Since the triangle is an equilateral triangle, the axis of the parabola bisects the angle at $30^\circ$.
From the figure, we can have one coordinate of the triangle as $\left( {2{t^2},4t} \right)$.
Thus, we can calculate the value of $\tan \left( {30^\circ } \right)$ and determine the value of $t$.
Hence,

$$\Rightarrow \tan 30 = \dfrac{{4t}}{{2{t^2}}} \\\ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{4t}}{{2{t^2}}} \\\ \Rightarrow t = 2\sqrt 3 \\\$$

Thus, the value of $t = 2\sqrt 3$
Hence, we will find the point $\left( {2{t^2},4t} \right)$ by substituting the value of $t = 2\sqrt 3$.
The point thus becomes, $\left( {24,8\sqrt 3 } \right)$.
Now, we will find the length of the side by applying the distance formula between the coordinates $\left( {0,0} \right)$ and $\left( {24,8\sqrt 3 } \right)$.
Thus, we have,

$$\Rightarrow d = \sqrt {{{\left( {24 - 0} \right)}^2} + {{\left( {8\sqrt 3 - 0} \right)}^2}} \\\ \Rightarrow d = \sqrt {576 + 192} \\\ \Rightarrow d = \sqrt {768} \\\ \Rightarrow d = 16\sqrt 3 \\\$$

Hence, the length of the side is $16\sqrt 3$.
Thus, option B is correct.

Note: We have used the distance formula, $d = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}}$. We can find the value of $a$ by comparing the value of ${y^2} = 8x$ with ${y^2} = 4ax$. Constructing a figure is important as it gives the value of coordinates easily. The equilateral triangle has the angle 60 degrees each and as the axis of parabola cuts it from the middle hence, we get the value of angle as $30^\circ$.