Question

An equilateral triangle is inscribed in a circle of radius 6cm. Find its side.

Answer 1

Hint: Draw the figure. The line connecting the centre of the circle to the vertex of the triangle is taken as radius. Draw perpendicular to the base of the triangle. Solve the triangle using Pythagoras theorem and find the length of the side.

Complete step-by-step answer:
Let ABC be an equilateral triangle inscribed in a circle of radius of 6cm.
Let us consider O as the centre of the circle.

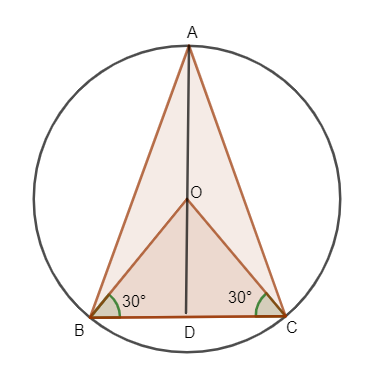
OA, OB and OC correspond to the radius of the circle.
OA=OB=OC=r
OA=OB=OC=6cm.
Let OD be a perpendicular from 0 to side BC.
So D becomes the mid-point of BC. So, OB and OC are bisectors of $\angle B$ and $\angle C$ respectively.
For an Equilateral triangle all angles as $60{}^\circ$,
$\therefore$For $\Delta ABC$,
$\angle A=\angle B=\angle C=60{}^\circ$
As OB and OC bisects angle$\angle B$ and $\angle C$, their angle becomes half of $\angle B$ and $\angle C$.
$\therefore \angle OBD=\angle OCD=\dfrac{60{}^\circ }{2}=30{}^\circ$
Now let us consider $\Delta OBD$, from the figure.
We know the angle=$30{}^\circ$and length of OB=6cm.
By using basic trigonometry we know that,
$\cos 30=\dfrac{BD}{6}$
$\Rightarrow$Length of BD = $6\times \cos 30.$
We know, $\cos 30=\dfrac{\sqrt{3}}{2}$
$\therefore$BD= $\dfrac{6\times \sqrt{3}}{2}=3\sqrt{3}$
BC=2BD
Because $\Delta OBD$ is equal to $\Delta ODC.$
Length BD=length DC.
Total length BC= BD+DC.
BC=BD+BC
BC=2BD
BC=$2\times 3\sqrt{3}=6\sqrt{3}$cm.
As it is an equilateral triangle,
AB=BC=AC=$6\sqrt{3}$cm

Note: If the question was given for isosceles triangle instead of equilateral triangle, the OA$\ne$OB$\ne$OC $\ne$radius. The angle will vary in case of isosceles triangle.