Question

An equilateral prism $ABC$ is placed in air with its base side $BC$ lying horizontally along $x$-axis as shown in the figure. A ray given by $\sqrt{3}z+x=10$ is incident at a point $P$ on face $AB$ of prism. Which of the following option(s) is/are correct?

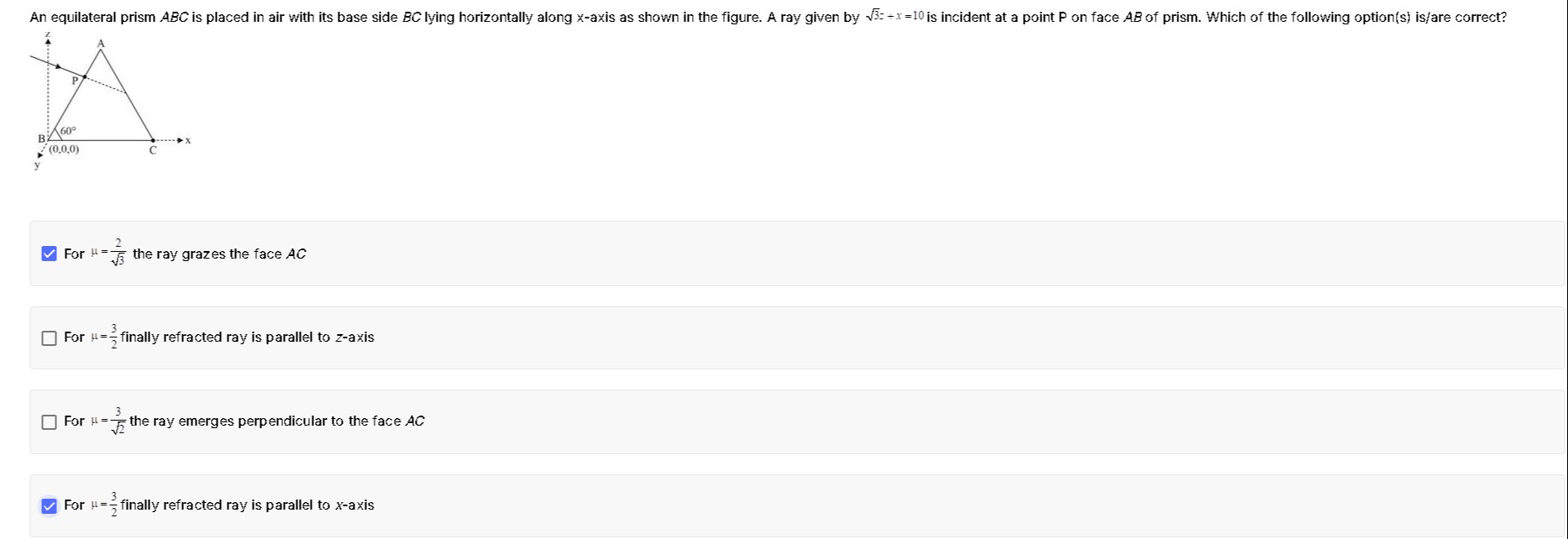
• A. For $\mu = \frac{2}{\sqrt{3}}$ the ray grazes the face $AC$
• B. For $\mu = \frac{3}{2}$ finally refracted ray is parallel to $z$-axis
• C. For $\mu = \frac{3}{\sqrt{2}}$ the ray emerges perpendicular to the face $AC$
• D. For $\mu = \frac{3}{2}$ finally refracted ray is parallel to $x$-axis

Answer 1

Answer: (A), (D)

For $\mu = \frac{2}{\sqrt{3}}$ the ray grazes the face $AC$ and For $\mu = \frac{3}{2}$ the finally refracted ray is parallel to the $x$-axis

Answer 2

The prism has an equilateral triangular cross‐section with base BC along the x‑axis and with ∠ABC = 60°. We locate B at the origin, C = (L, 0, 0) and A = (L/2, (√3/2)L, 0). The given ray in air has equation

$$\sqrt{3}z + x = 10.$$

Its plane of propagation is the $xz$–plane.

• When the ray is incident on face AB and “grazes” the face AC at a later point in the prism, the incidence at face AC is exactly at the critical angle. A geometric–optical analysis yields the condition

$$\mu=\frac{2}{\sqrt{3}}.$$

• With a different value of $\mu$, when $\mu=\frac{3}{2}$ the ray, after being refracted at both surfaces, emerges parallel to the $x$–axis.