Question

An equiconvex lens of glass of focal length 0.1 m is cut along a plane perpendicular to the principal axis into two equal parts. The ratio of focal length of new lenses formed is
${\text{A}}{\text{. 1:1}} \\\ {\text{B}}{\text{. 1:2}} \\\ {\text{C}}{\text{. 2:1}} \\\ {\text{D}}{\text{. 2:}}\dfrac{1}{2} \\\$

Answer 1

Using the lens maker formula, we can study the lenses of any shape and refracting surface. By comparing the lens maker formula for initial biconvex lens and final cut lens, we can find the ratio of their focal lengths.

Formula used: The lens maker formula is given as
$\dfrac{1}{f} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
where f is the focal length of the lens, $\mu$ signifies the refractive index of the material of the lens, ${R_1}$ and ${R_2}$ are the radius of curvatures of the two refracting surfaces of the lens.

Complete step by step answer:

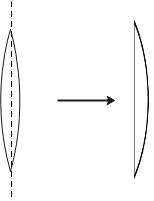
The lens maker formula can be used to study the given lenses. The first lens is biconvex and the two refracting surfaces have the same radii of curvature which is equal to 0.1 m. Therefore we can write the lens maker formula for first lens as follows:

$\dfrac{1}{{{f_{initial}}}} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{ + R}} - \dfrac{1}{{ - R}}} \right) \\\ = \left( {\mu - 1} \right)\left( {\dfrac{1}{R} + \dfrac{1}{R}} \right) \\\ = \left( {\mu - 1} \right)\left( {\dfrac{2}{R}} \right){\text{ }}...{\text{(i)}} \\\$

Now this lens is cut into half from the middle along the plane perpendicular to the principal axis of the lens. Therefore one refracting surface is convex while the other refracting surface is plane. The radius of curvature of the convex side is the same as before but the radius of curvature of the plane side is at infinity. Therefore, we can write the lens maker formula for the new lens as follows:

$\dfrac{1}{{{f_{final}}}} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{ + R}} - \dfrac{1}{\infty }} \right) \\\ = \left( {\mu - 1} \right)\left( {\dfrac{1}{R}} \right){\text{ }}...{\text{(ii)}} \\\$

Now, by dividing the equation (i) with equation (ii), we get

$\dfrac{{{f_{final}}}}{{{f_{initial}}}} = \dfrac{{\left( {\mu - 1} \right)\left( {\dfrac{2}{R}} \right){\text{ }}}}{{\left( {\mu - 1} \right)\left( {\dfrac{1}{R}} \right)}} \\\ \Rightarrow \dfrac{{{f_{final}}}}{{{f_{initial}}}} = \dfrac{2}{1} = 2:1 \\\$
Hence, the correct answer is option C.

Note:
1. All distances to the left of the lens are taken to be negative while all distances to the right of the lens are taken to be negative.
2. The focus is defined on the basis of curvature of the front circle of the lens. A concave lens has negative focus because it lies on the left side of the lens while a convex lens has positive focus because it lies on the right side of the lens.