Solveeit Logo
Login

Question

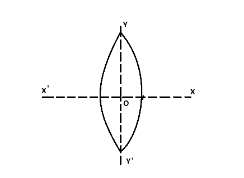
Question: An equiconvex lens is cut into two halves a long (i) \(XOX'\) and (ii) \(YOY'\) as shown in the figu...

An equiconvex lens is cut into two halves a long (i) XOX′XOX' and (ii) YOY′YOY' as shown in the figure let f, f′f', f′′f'' be the focal lengths of the complete lens of each half in case (i) and of each half in case (ii) respectively
Choose the correct statement from the following :

A. f′=f,f′′=ff' = f,f'' = f
B. f′=2f,f′′=2ff' = 2f,f'' = 2f
C. f′=f,f′′=2ff' = f,f'' = 2f
D. f′=2f,f′′=ff' = 2f,f'' = f

Explanation

Solution

To solve this question, we will use the lens maker’s formula, which states that the relation connecting the focal length of the lens with the radii of curvature and its two surfaces and the refractive index of the material of the lens is given by, 1f=(μ−1)(1R1−1R2)\dfrac{1}{f} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)

Complete answer:
Given that,
f, f′f', f′′f'' are the focal lengths of the complete lens of each half in case (i) and of each half in case (ii) respectively.
According to the lens maker’s formula,
The focal length of the equiconvex lens is given by,
1f=(μ−1)(1R1−1R2)\dfrac{1}{f} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right) ……. (i)

We know that,
For an equiconvex lens, R1=R2=R{R_1} = {R_2} = R, but we will take R2{R_2} as negative because the directions are opposite.
Putting this in equation (i), we will get
⇒1f=(μ−1)(1R−1(−R))\Rightarrow \dfrac{1}{f} = \left( {\mu - 1} \right)\left( {\dfrac{1}{R} - \dfrac{1}{{\left( { - R} \right)}}} \right)
⇒1f=(μ−1)2R\Rightarrow \dfrac{1}{f} = \left( {\mu - 1} \right)\dfrac{2}{R} ….. (ii)

Now, we will take 2 cases,

Case 1: when the lens is cut along XOX′XOX', then the radii of curvature of each surface of the lens remain unchanged, i.e. R1=+R,R2=−R{R_1} = + R,{R_2} = - R
Put this in equation (i), we will get
⇒1f′=(μ−1)(1R−1(−R))\Rightarrow \dfrac{1}{{f'}} = \left( {\mu - 1} \right)\left( {\dfrac{1}{R} - \dfrac{1}{{\left( { - R} \right)}}} \right)
⇒1f′=(μ−1)2R=1f\Rightarrow \dfrac{1}{{f'}} = \left( {\mu - 1} \right)\dfrac{2}{R} = \dfrac{1}{f}
Equating this with equation (ii), we will get
⇒f′=f\Rightarrow f' = f

Case 2: when the lens is cut along YOY′YOY', then a half portion of the lens becomes a plano-convex lens and R1=+R,R2=∞{R_1} = + R,{R_2} = \infty
Putting this in equation (i),
⇒1f′′=(μ−1)(1R−1∞)\Rightarrow \dfrac{1}{{f''}} = \left( {\mu - 1} \right)\left( {\dfrac{1}{R} - \dfrac{1}{\infty }} \right)
⇒1f′′=(μ−1)1R=12f\Rightarrow \dfrac{1}{{f''}} = \left( {\mu - 1} \right)\dfrac{1}{R} = \dfrac{1}{{2f}}
Equating this with equation (ii), we get
⇒f′′=2f\Rightarrow f'' = 2f

So, the correct answer is “Option C”.

Note:
Whenever we ask such questions, we have to remember the lens maker’s formula. First, we will find out the focal length of the equiconvex lens. Then we will make two cases, i.e. when the lens is cut along XOX′XOX' and when the lens is cut along YOY′YOY'. After that, we will find out the focal length in both the cases and by equating them with the focal length of the equiconvex lens, we will get the relation between the focal length in each case. Through this, we will get the answer.