Solveeit Logo
Login

Question

Question: An equiconcave lens of glass and focal length of 20 cm is halved and kept at separation of 10 mm apa...

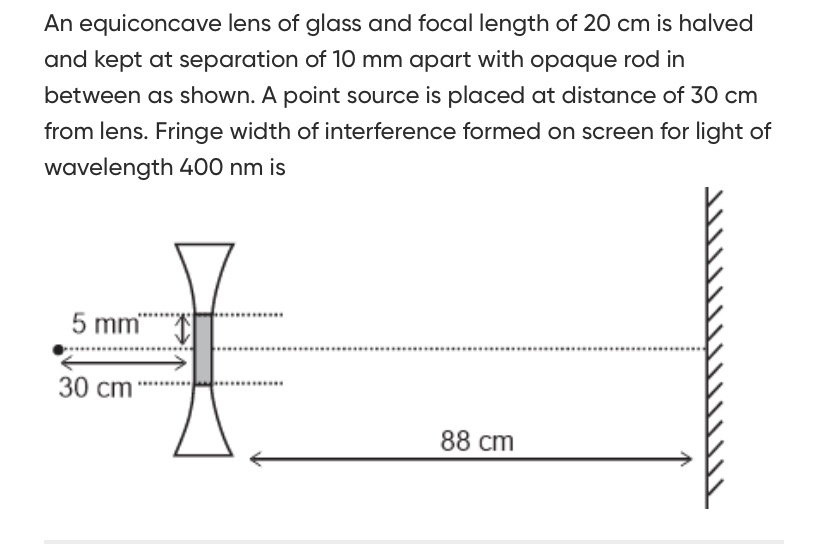
An equiconcave lens of glass and focal length of 20 cm is halved and kept at separation of 10 mm apart with opaque rod in between as shown. A point source is placed at distance of 30 cm from lens. Fringe width of interference formed on screen for light of wavelength 400 nm is

Answer

0.04 mm

Explanation

Solution

The problem describes a setup analogous to Young's double-slit experiment where the two halves of an equiconcave lens act as sources of coherent virtual images.

  1. Image Formation: The lens formula is 1v−1u=1f\frac{1}{v} - \frac{1}{u} = \frac{1}{f}. Given: Focal length f=−20f = -20 cm (equiconcave), object distance u=−30u = -30 cm. 1v=1f+1u=1−20 cm+1−30 cm=−3−260 cm=−560 cm=−112 cm\frac{1}{v} = \frac{1}{f} + \frac{1}{u} = \frac{1}{-20 \text{ cm}} + \frac{1}{-30 \text{ cm}} = \frac{-3 - 2}{60 \text{ cm}} = \frac{-5}{60 \text{ cm}} = \frac{-1}{12 \text{ cm}} The virtual images are formed at v=−12v = -12 cm from the lens.

  2. Separation of Virtual Sources: The lateral magnification m=vu=−12 cm−30 cm=25m = \frac{v}{u} = \frac{-12 \text{ cm}}{-30 \text{ cm}} = \frac{2}{5}. The two halves of the lens are separated by 10 mm. This separation directly translates to the separation of the virtual sources (dd) because the point source is on the principal axis. Thus, d=10d = 10 mm.

  3. Distance to Screen: The virtual sources are at 12 cm in front of the lens. The screen is placed 88 cm behind the lens. The total distance from the virtual sources to the screen is D=12 cm+88 cm=100 cmD = 12 \text{ cm} + 88 \text{ cm} = 100 \text{ cm}.

  4. Fringe Width Calculation: The fringe width β\beta is given by β=λDd\beta = \frac{\lambda D}{d}. Given: Wavelength λ=400 nm=400×10−9 m\lambda = 400 \text{ nm} = 400 \times 10^{-9} \text{ m}. D=100 cm=1 mD = 100 \text{ cm} = 1 \text{ m}. d=10 mm=0.01 md = 10 \text{ mm} = 0.01 \text{ m}. β=(400×10−9 m)×(1 m)0.01 m=400×10−910−2 m=400×10−7 m=4×10−5 m\beta = \frac{(400 \times 10^{-9} \text{ m}) \times (1 \text{ m})}{0.01 \text{ m}} = \frac{400 \times 10^{-9}}{10^{-2}} \text{ m} = 400 \times 10^{-7} \text{ m} = 4 \times 10^{-5} \text{ m} Converting to millimeters: β=4×10−5 m×1000 mm1 m=0.04 mm\beta = 4 \times 10^{-5} \text{ m} \times \frac{1000 \text{ mm}}{1 \text{ m}} = 0.04 \text{ mm}