Question

An engine of power $58.8kW$ pulls a train of mass $2 \times {10^5}kg$ with velocity $36km{h^{ - 1}}$. The coefficient of friction is;
A) $0.3$
B) $0.03$
C) $0.003$
D) $0.0003$
E) $0.04$

Answer 1

Velocity is the ratio of displacement to time. According to the given condition the velocity is constant and so the net acceleration of the train is zero.

Complete step by step solution:
Here, we have a train which is pulled by an engine of power $58.8kW$.
The power in Watt will be $P = 58.8 \times {10^3} = 58800W$
Also, the mass of the train is given as $m = 2 \times {10^5}kg$
So let us understand the situation with the help of an FBD.

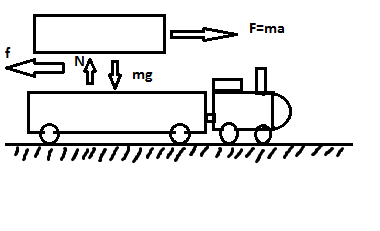
The diagram above shows the free body diagram (FBD)
Let us balance the all the forces;
In the X direction;
$F = f$ (equation: 1)
In the Y direction;
$N = mg$ (equation: 2)
Also we know that by definition frictional force can be written as;
$f = \mu N$ (equation: 3)
Hence from equation 2 and equation 3 we have;
$F = \mu mg$ (Equation: 4)
Now we all know that,
Power is the work done per unit time, so mathematically we can write;
$P = \dfrac{W}{t}$ (Equation: 5)
And we all know that,
Work is the product of force applied on the body and the displacement that has occurred due to that force;
So mathematically we can say;
$W = F.x$(equation: 6)
Now from equation 5 and equation 6 we get;
$P = \dfrac{{F.x}}{t}$
Now we all know that the velocity is the ratio of displacement to time we have;
$v = \dfrac{x}{t}$
Thus we have,
$P = F.v$
Substituting the values we get;
$58800 = \dfrac{F}{{36 \times 1000}} \times 3600$
$\Rightarrow F = 5880N$
Now, from equation 4 we get
$\Rightarrow \mu mg = 5880$
$\Rightarrow \mu = \dfrac{{5880}}{{mg}}$
$\Rightarrow \mu = \dfrac{{5880}}{{2 \times {{10}^5} \times 10}}$
$\therefore \mu = 0.03$

Therefore, option B is correct.

Note: The velocity is constant that means there is no net acceleration.
This is because all forces on the body are balancing each other.
So by simply solving the force equations derived from the FBD, we can solve the question.