Question

An engine of 150 kW power is drawing a train of total mass 150,000 kg up an inclination of 1 in 5. The frictional resistance is 4 kg wt/1000 kg. Find its maximum speed. Given: $g = 10\,{\text{m/}}{{\text{s}}^2}$.

Answer 1

Determine the frictional force on the total mass of the train in units of newton. Draw the free body diagram and determine the net resistance force in the backward direction. The power is the product of force and velocity.

Formula used:
Power, $P = Fv$,
where, F is the force and v is the velocity.

Complete step by step answer:
We have given the power of the engine drawing the train $P = 150\,{\text{kW}} = 1.5 \times {10^5}\,{\text{W}}$, the mass of the train $m = 150,000\,{\text{kg}} = 1.5 \times {10^4}\,{\text{kg}}$ and the inclination of the plane is $\sin \theta = \dfrac{1}{5}$.
The given resistance force due to the friction is 4 kg-wt per 1000 kg. Therefore, the total resistance force on the total mass of the train will be,
${f_r} = \dfrac{{4 \times 150000}}{{1000}}$
$\Rightarrow {f_r} = 600\,{\text{kg - wt}}$
$\Rightarrow {f_r} = 600 \times 10\,{\text{N}}$
$\Rightarrow {f_r} = 6000\,{\text{N}}$

Let us draw the free body diagram of the forces acting on the train as follows,

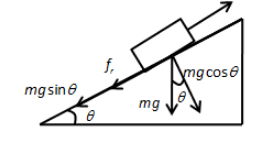
From the above figure, the total resistance force in the backward direction is,
$F = mg\sin \theta + {f_r}$
Substituting $m = 1.5 \times {10^4}\,{\text{kg}}$, $g = 10\,{\text{m/}}{{\text{s}}^2}$ , $\sin \theta = \dfrac{1}{5}$ and ${f_r} = 6000\,{\text{N}}$ in the above equation, we get,
$F = \left( {1.5 \times {{10}^5}} \right)\left( {10} \right)\left( {\dfrac{1}{5}} \right) + 6000$
$\Rightarrow F = 3.06 \times {10^5}\,{\text{N}}$

The power of the engine to draw the train with this backward resistance force is,
$P = Fv$
$\Rightarrow v = \dfrac{P}{F}$
Here, v is the velocity of the train.
Substituting $P = 1.5 \times {10^5}\,{\text{W}}$ and $F = 3.06 \times {10^5}\,{\text{N}}$ in the above equation, we get,
$v = \dfrac{{1.5 \times {{10}^5}\,{\text{W}}}}{{3.06 \times {{10}^5}\,{\text{N}}}}$
$\Rightarrow v = 0.49\,{\text{m/s}}$
$\therefore {\text{v}} \approx {\text{0}}{\text{.5}}\,{\text{m/s}}$

Thus, the maximum speed of the train is 0.50 m/s.

Note: The crucial step in this solution is to determine the frictional resistance since it is given in kg-wt. You may wonder what kg-wt is. 1 kg-wt is the force equivalent to a weight of 1 kg body that is 9.8 N or 10 N as given in the question. If the inclination is given as 1 in 5, it is always the sine angle of ratio of 1 and 5, and not the cosine angle. Students must always draw the free body diagram to determine the direction of forces.