Question

An engine approaches a hill with constant speed. When it is at a distance of $0.9km$ , it blows a whistle, when echo is heard by the driver after $5s$ . If the speed of sound in air is $330m{s^{ - 1}}$ then speed of engine is-
(A) $10m{s^{ - 1}}$
(B) $20m{s^{ - 1}}$
(C) $30m{s^{ - 1}}$
(D) $40m{s^{ - 1}}$

Answer 1

Hint : Here, the engine is approaching towards the hill and we have to calculate the distance when the driver hears its whistle’s echo. But we must understand the concept that when the engine approaches the hill it blows a whistle when it is at $t = 0$ and after $t = 5\sec$ it hears the echo. So between this time the engine has travelled the distance and you have to calculate that distance and then the speed will be calculated.

Complete Step By Step Answer:
Let, the speed of the engine be $v$ and time be $t$ and the distance be $d$
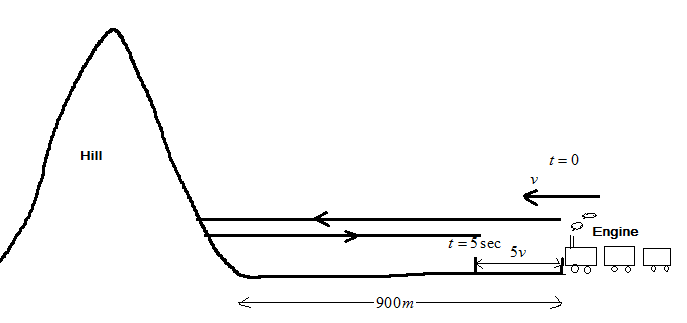
Thus, the distance between the engine at time $t = 0$ is $0.9km = 900m$ and we have to calculate the distance between the hill and the engine at $t = 5\sec$ . As shown in figure below the echo the whistle was approached the driver after $5\sec$ is given by
Distance travelled by the whistle in $5\sec$ is given by
$d = 900 + (900 - 5v)$
$\Rightarrow d = 1800 - 5v$ ….. $(1)$

We have been given the speed of the sound as ${v_S} = 330m{s^{ - 1}}$
Thus, the distance travelled by the sound is
$d = {v_S} \times 5$ …. $(2)$
$\Rightarrow 1800 - 5v = 330 \times 5$ ….. (on equating $(1)$ and $(2)$ )
$\Rightarrow 1800 - 5v = 1650$
$\Rightarrow 5v = 150$
$\Rightarrow v = 30m{s^{ - 1}}$
The speed of the engine is $30m{s^{ - 1}}$
The correct answer is the option C.

Note :
We know that the speed of sound is given and time is given in which it returns to the driver so it was easier to solve this problem and find distance travelled by the sound. Thus we have to be careful about calculating the distance and speed of the engine as we have solved in the above question.