Question

An empty plastic box of mass $M$ is found to accelerate up at the rate of ($\dfrac{g}{8}$) when placed deep inside water. What mass of pebbles be put inside the plastic box so that it may accelerate down at the rate of $\dfrac{g}{8}$ is
A. $0.5M$
B. $0.25M$
C. $M$
D. $\left( {2M} \right)/7$

Answer 1

Use the expression for Newton’s second law of motion. Apply Newton’s second law of motion to the empty plastic box to determine the upward buoyant force acting on the box. Apply Newton’s second law of motion to the plastic box with pebbles in the upward direction and determine the required mass of the pebbles.

Formula used:
The expression for Newton’s second law of motion is given by
${F_{net}} = ma$
Here, ${F_{net}}$ is net force acting on the object, $m$ is mass of the object and $a$ is acceleration of the object.

Complete step by step answer:
We have given that the empty plastic box of mass $M$ is accelerating in the upward direction when it is placed inside deep water. The acceleration of the empty plastic box inside the water is $\dfrac{g}{8}$ in the upward direction.
$a = \dfrac{g}{8}$

Let us draw a free body diagram of the empty plastic box.

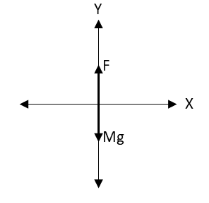
In the above free body diagram, $Mg$ is the weight of the empty plastic box and $F$ is the upward buoyant force acting on the plastic box.

Let us first determine the buoyant force acting on the empty plastic box in the upward direction. Apply Newton’s second law of motion to the empty plastic box in the upward direction.
$F - Mg = M\dfrac{g}{8}$
$\Rightarrow F = M\dfrac{g}{8} + Mg$
$\Rightarrow F = \dfrac{9}{8}Mg$
Hence, the upward buoyant force acting on the empty plastic box is $\dfrac{9}{8}Mg$.

We want the plastic box to accelerate in the downward direction with acceleration $\dfrac{g}{8}$ when the pebbles of mass $m$ are added in the plastic box.
Apply Newton’s second law of motion to the empty plastic box in the upward direction.
$F - \left( {M + m} \right)g = - \left( {M + m} \right)\dfrac{g}{8}$
Substitute $\dfrac{9}{8}Mg$ for $F$ in the above equation.
$\Rightarrow \dfrac{9}{8}Mg - \left( {M + m} \right)g = - \left( {M + m} \right)\dfrac{g}{8}$
$\Rightarrow \dfrac{9}{8}M - M - m = - \dfrac{M}{8} - \dfrac{m}{8}$
$\Rightarrow \left( {\dfrac{1}{8} - 1} \right)m = \left( { - \dfrac{1}{8} - \dfrac{9}{8} + 1} \right)M$
$\Rightarrow \left( {\dfrac{{ - 7}}{8}} \right)m = \left( {\dfrac{{ - 1 - 9 + 8}}{8}} \right)M$
$\Rightarrow m = \left( { - \dfrac{2}{8}} \right)\left( { - \dfrac{8}{7}} \right)M$
$\therefore m = \dfrac{2}{7}M$
Therefore, the mass of the pebbles that must be added in the plastic box is $\dfrac{2}{7}M$.

Hence, the correct option is D.

Note: The students may think that the sign of acceleration of the plastic box with pebbles is taken negatively while applying Newton’s second law of motion. The acceleration of the plastic box with pebbles is in the downward direction. Hence, its sign is taken negative and positive for the empty box with its acceleration in the upward direction.