Question

An e.m.f. $E = E_0 \cos \omega t$ is applied to the $L-R$ circuit. The inductive reactance is equal to the resistance '$R$' of the circuit. The power consumed in the circuit is

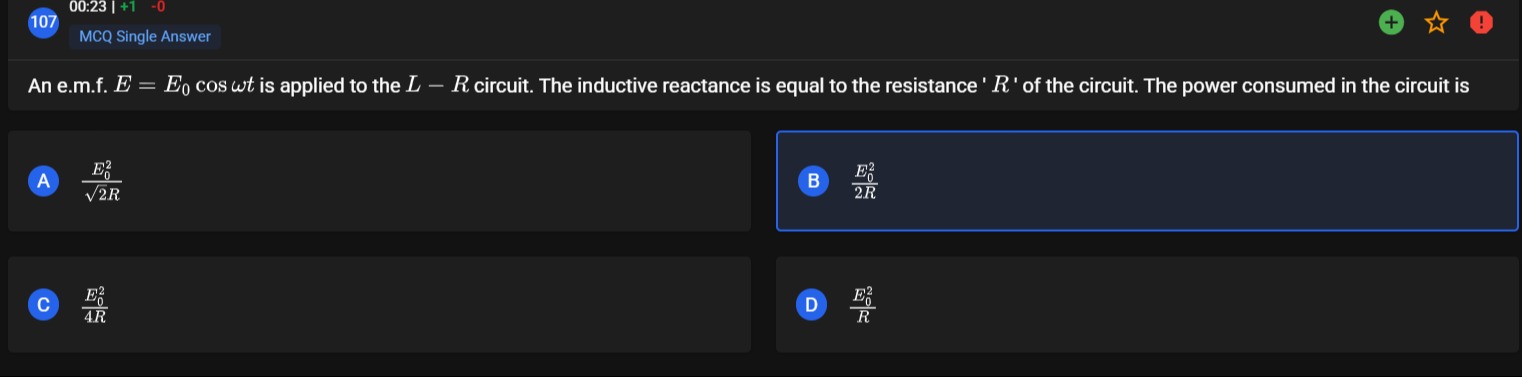
• A. $\frac{E_0^2}{\sqrt{2}R}$
• B. $\frac{E_0^2}{2R}$
• C. $\frac{E_0^2}{4R}$
• D. $\frac{E_0^2}{R}$

Answer 1

Answer: (C)

$\frac{E_0^2}{4R}$

Answer 2

Solution:

1. Impedance Calculation:
   Given $X_L = R$, the total impedance is

   $$Z = \sqrt{R^2 + (X_L)^2} = \sqrt{R^2 + R^2} = \sqrt{2}\,R.$$

2. Peak Current:
   From the applied emf $E = E_0 \cos\omega t$, the peak current is

   $$I_0 = \frac{E_0}{Z} = \frac{E_0}{\sqrt{2}\,R}.$$

3. Average Power Dissipated:
   Only the resistor dissipates power. The average power is

   $$P_{\text{avg}} = \frac{1}{2} I_0^2 R = \frac{1}{2}\left(\frac{E_0}{\sqrt{2}\,R}\right)^2 R = \frac{1}{2}\left(\frac{E_0^2}{2R^2}\right)R = \frac{E_0^2}{4R}.$$

Core Explanation:

• Total impedance: $Z = \sqrt{2}\,R$.
• Peak current: $I_0 = \frac{E_0}{\sqrt{2}\,R}$.
• Average power: $P_{\text{avg}} = \frac{E_0^2}{4R}$.