Question
Question: An elliptically shaped ring of dimensions shown in figure just touches the horizontal surface of a l...
An elliptically shaped ring of dimensions shown in figure just touches the horizontal surface of a liquid of surface tension S. The force required to pull the ring away from the liquid surface is
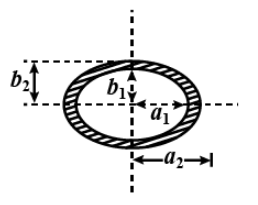
(A) 2π(a1b1+a2b2)S
(B) π(a1+b1+a2+b2)S
(C) π(2a1+a2+2b1+b2)S
(D) 2π(a1b1+a2b2)S
Solution
Here first we find the internal mean radius and also the circumference of the ring. Then we again find the external mean radius and external circumference. Then we can get the force that is required by using the formula of surface tension.
Complete step by step answer:
Given,
An elliptically shaped ring of dimensions shown in figure just touches the horizontal surface of a liquid of surface tension S.
The mean radius of the inner ring is
r1=a1b1
Now, the circumference of the inner ring is
2πr1=2π(a1b1)
The mean radius of the external ring is
r2=a2b2
The circumference of the outer ring is
2πr2=2π(a2b2)
To find the force we have to add the circumferences of the ring and multiply with surface tension S.
So, the required force=2π(a1b1+a2b2)S
Hence, option A is the correct answer.
Additional information:
Surface tension: The attractive force exerted by the molecules below on the surface molecules of a liquid appears to pull the surface molecules into the bulk of the liquid and makes the liquid adopt the form that has the least surface area.The ratio of the surface force F to the length L along which the force exists is known as surface tension. Mathematically, surface tension is written as-
S=F/L
The results of intermolecular forces at the interface create surface tension. Surface tension depends on the composition of the material, temperature and the ambient environment. Liquids were molecules that would have a high surface tension and strong attractive intermolecular forces.
Note: Here while calculating the radius we have to see that we are calculating the mean radius. So, we have to put the total radius under square root.
