Question

An ellipse passing through the point $\left( 2\sqrt{13},4 \right)$ has its foci at $\left( -4,1 \right)$ and $\left( 4,1 \right)$ , then its eccentricity is
(a) $\dfrac{2}{3}$
(b) $\dfrac{1}{3}$
(c) $\dfrac{1}{4}$
(d) $\dfrac{1}{2}$

Answer 1

The formula of eccentricity, can be given as, $XY=2ae$. So, first of all we will find the value of XY using the distance formula. Then we will find value of $2a$ by using the fact that length of major axis is equal to the distance between focus and point on ellipse, which can be given mathematically as, ${{d}_{1}}+{{d}_{2}}=2a$. Now, again using the distance formula we will find the distance of XP and YP and from that we will find the value of $2a$ and then substitute all the values in expression of eccentricity and we will find our answer.

Complete step by step answer:
In question we are given that an ellipse having its foci at $\left( -4,1 \right)$ and $\left( 4,1 \right)$ passes through the point $\left( 2\sqrt{13},4 \right)$. And we are asked to find the eccentricity, so first of all we will draw a figure for our simplicity,

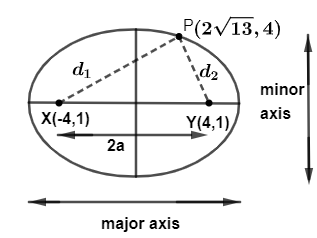
Now, the eccentricity can be given be given by the formula as,
$XY=2ae$ ……………..(i)
Where, XY is the distance between two foci, e is eccentricity, 2a is length of major axis
Now value of XY can be given by distance formula, which can be given as,
$XY=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$ ……………(ii)
Here, $\left( {{x}_{1}},{{y}_{1}} \right)=\left( -4,1 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)=\left( 4,1 \right)$, on substituting these values in expression (ii) we will get,
$XY=\sqrt{{{\left( -4-4 \right)}^{2}}+{{\left( 1-1 \right)}^{2}}}=\sqrt{{{\left( -8 \right)}^{2}}+0}=8$ …………….(iii)
Now, we know that distance between two foci is equal to the distance between one focus and the point through which the ellipse passes, it can be seen mathematically as,
${{d}_{1}}+{{d}_{2}}=2a$ ……………….(iv)
Here, from figure we can see that ${{d}_{1}}$ is the distance between points X and P i.e. XP and ${{d}_{2}}$ is the distance between points Y and P i.e. YP, so the expression (iv) can also be written as,
$XP+YP=2a$……………(v)
Now, again using the distance formula to find value of XP, where $\left( {{x}_{1}},{{y}_{1}} \right)=\left( -4,1 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)=\left( 2\sqrt{13},4 \right)$, so on substituting the values in distance formula we will get,
$XP=\sqrt{{{\left( -4-4\sqrt{13} \right)}^{2}}+{{\left( 1-4 \right)}^{2}}}$
On expanding the terms and simplifying further we will get
$XP=\sqrt{16+16\sqrt{13}+52+9}=\sqrt{77+16\sqrt{3}}$
Now, 77 can also be written as $64+13$ and $16\sqrt{13}$ can be written as $2\times 8\times \sqrt{13}$, so replacing the values in expression we will get,
$XP=\sqrt{64+13+2\times 8\times \sqrt{13}}$
Now, on rearranging the terms the expression will be, $XP=\sqrt{64+2\times 8\times \sqrt{13}+13}$, which is square of $\left( 8+\sqrt{13} \right)$, so again replacing the value in expression we will get,
$XP=\sqrt{{{\left( 8+\sqrt{13} \right)}^{2}}}=8+\sqrt{13}$ ……………(vi)
Same way, on applying the distance formula for YP, where $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 4,1 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)=\left( 2\sqrt{13},4 \right)$, so on substituting the values in distance formula we will get,
$YP=\sqrt{{{\left( 4-4\sqrt{13} \right)}^{2}}+{{\left( 1-4 \right)}^{2}}}$
On expanding the terms and simplifying further we will get,
$YP=\sqrt{16-16\sqrt{13}+52+9}=\sqrt{77-16\sqrt{3}}$
So, again applying the same method as above, $\sqrt{77-16\sqrt{3}}$ can be written as $\sqrt{{{\left( 8-\sqrt{13} \right)}^{2}}}$, on replacing the values we will get,
$YP=\sqrt{{{\left( 8-\sqrt{13} \right)}^{2}}}=8-\sqrt{13}$ ………….(vii)
Now, on substituting the values of expression (vi) and (vii) in expression (v) we will get,
$8+\sqrt{13}+8-\sqrt{13}=2a$
$\Rightarrow 8+8=2a\Rightarrow 16=2a$
Now, on replacing the value of $2a$ in expression (i) and substituting the value of XY from expression (ii) we will get,
$8=16e$
$\Rightarrow e=\dfrac{8}{16}=\dfrac{1}{2}$
Thus, the value of eccentricity is $\dfrac{1}{2}$.
Hence, option (d) is the correct answer.

Note: In distance formula, if we consider point Y as $\left( {{x}_{1}},{{y}_{1}} \right)$ and X as $\left( {{x}_{2}},{{y}_{2}} \right)$, then $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 4,1 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)=\left( -4,1 \right)$, on substituting these values in distance formula we will get,
$XY=\sqrt{{{\left( 4-\left( -4 \right) \right)}^{2}}+{{\left( 1-1 \right)}^{2}}}=\sqrt{{{\left( 4+4 \right)}^{2}}+0}=8$ . So, we can say that we can consider any point as $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$, the final answer does not change. So, this can be considered as an alternate way to find answers to the distance formula. Also, do not make calculation mistakes as it is a long sum to solve so many times calculation errors happen. So, be careful while solving it.