Question

An ellipse is drawn by taking a diameter of the circle ${{(x-1)}^{2}}+{{y}^{2}}=1$ as its semi-minor axis and a diameter of the circle ${{x}^{2}}+{{(y-2)}^{2}}=4$ is semi-major axis. If the Centre of the ellipse is at the origin and its axes are the coordinate axes, then the equation of the ellipse is
A) $4{{x}^{2}}+{{y}^{2}}=4$
B) ${{x}^{2}}+4{{y}^{2}}=8$
C) $4{{x}^{2}}+{{y}^{2}}=8$
D) ${{x}^{2}}+4{{y}^{2}}=16$

Answer 1

In this particular problem there are two equations in which we have to find the radius and diameter of each equation. The standard equation of a circle is $(x-h)^2 + (y-k)^2= r^2$, where $(h,k)$ is the center of the circle and $r$ is the radius of the circle.
The diameter of each equation is our a and b so that we can substitute this value in the general equation of the ellipse. General equation of ellipse is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.
Where the length of the semi major axis of the ellipse is $a$ and the length of the semi minor axis of the ellipse is $b$.

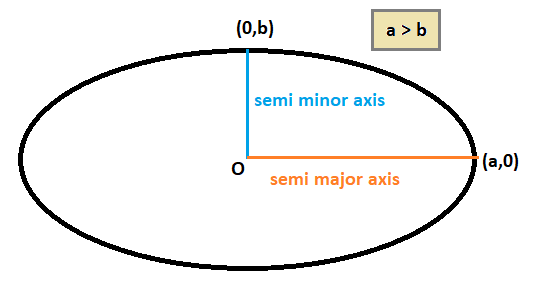
Image: Image showing an ellipse with the semi minor and semi major axis.

Complete step by step solution:
The equation which is given${{(x-1)}^{2}}+{{y}^{2}}=1$ that means we have to draw a circle with center $(1,0)$ and radius $1$.

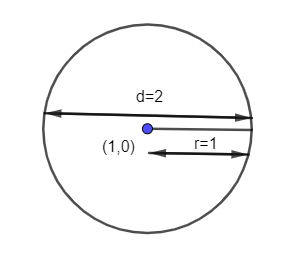
The diameter of this circle is $2 \times$ Radius = $2 \times 1 =2$
Given that, this diameter length is equal to the semi minor axis length of ellipse $(b)$= 2
Another circle equation which is given ${{x}^{2}}+{{(y-2)}^{2}}=4$. This circle has center $(0,2)$ and radius $2$.

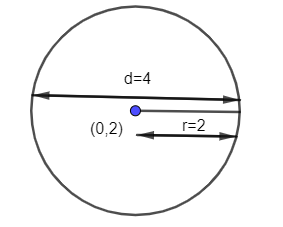
The diameter of this circle is $2 \times$ Radius = $2 \times 2 =4$
Given that, this diameter length is equal to the semi major axis length of ellipse $(a)$= 4
We were asked to find the equation of the ellipse.
So, we have to find the equation of ellipse in the form of $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.
After substituting the value of $a=4$ and $b=2$ in the above equation
$\dfrac{{{x}^{2}}}{{{4}^{2}}}+\dfrac{{{y}^{2}}}{{{2}^{2}}}=1$
After simplifying further we get:
$\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{4}=1$
Take LCM and simplify it we get:
$\dfrac{{{x}^{2}}+4{{y}^{2}}}{16}=1$
Multiply 16 on both side we get the final equation of an ellipse
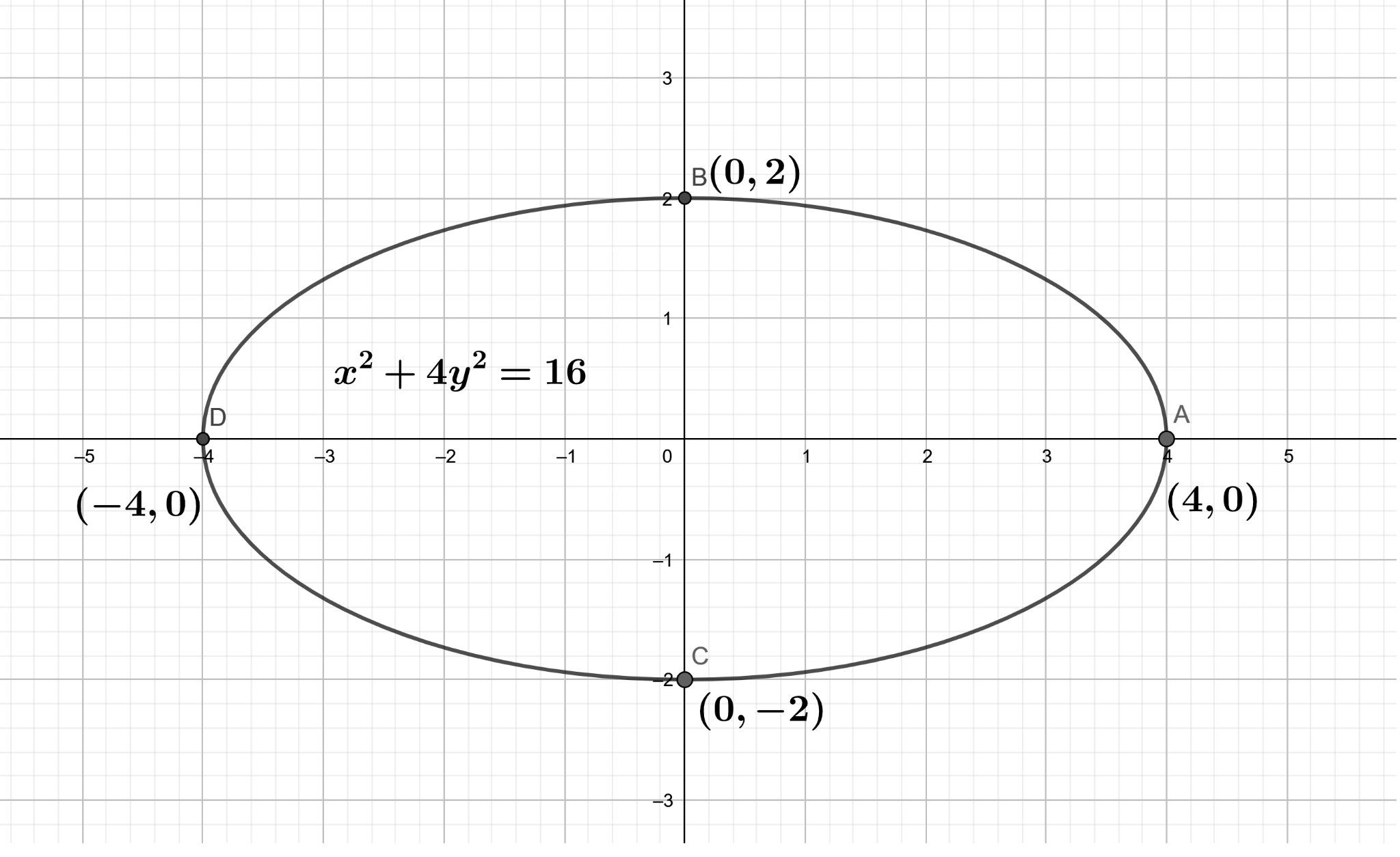
$\therefore {{x}^{2}}+4{{y}^{2}}=16$
Therefore, the correct option is “option D”.
The graph of the ellipse ${{x}^{2}}+4{{y}^{2}}=16$ is shown below.

Note:
In this particular problem there are two equations given and to find the radius we have to see the RHS of the given two which is ${{r}^{2}}$ from which we find the value of radius. Always remember the general equation because we need to remember such a general equation to find the equation of an ellipse. In general, the value of $a$ and $b$ which is nothing but the value of diameter.