Question

An ellipse is described by using an endless string which is passed over two pins. If the axes are 6cm and 4cm, the necessary length of the string and the distance between the pins respectively are (in cm) ?

Answer 1

The two pins are located on the two foci of the ellipse formed. Now, the lengths of the two axes are 6cm and 4cm respectively. So, we can calculate the distance between the two foci by calculating the eccentricity of the ellipse. Now, the necessary length of wire is equal to the circumference of the ellipse which is approximated by the formula: $\pi \left( a+b \right)$, where ‘a’ and ‘b’ are the lengths of the two axes.

Complete step by step answer:
Let us first of all derive the expression of the ellipse formed. The general expression for a standard ellipse is given by:
$\Rightarrow \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
In our problem, we have:
$\begin{aligned} & \Rightarrow a=6 \\\ & \Rightarrow b=4 \\\ \end{aligned}$
Putting it in the above equation, we get the equation of our ellipse as:
$\Rightarrow \dfrac{{{x}^{2}}}{{{6}^{2}}}+\dfrac{{{y}^{2}}}{{{4}^{2}}}=1$
Now, let us calculate the length of string necessary for the construction of this ellipse. This length is equal to the circumference of the ellipse and it can be calculated as follows:
Let the length of string required be ‘L’, then we have:
$\begin{aligned} & \Rightarrow L\approx \pi \left( a+b \right) \\\ & \Rightarrow L\approx 3.14\left( 6+4 \right)cm \\\ & \Rightarrow L\approx 3.14\times 10cm \\\ & \therefore L\approx 31.4cm \\\ \end{aligned}$
Therefore, the length of string comes out to be 31.4cm .
Now, we will calculate the distance between the two pins. This is equal to (2ae), where ‘e’ is the eccentricity of the ellipse and it can be calculated using the formula shown below:
$\begin{aligned} & \Rightarrow {{b}^{2}}={{a}^{2}}\left( 1-{{e}^{2}} \right) \\\ & \Rightarrow {{4}^{2}}={{6}^{2}}\left( 1-{{e}^{2}} \right) \\\ & \Rightarrow \dfrac{16}{36}=1-{{e}^{2}} \\\ & \Rightarrow {{e}^{2}}=1-\dfrac{16}{36} \\\ & \Rightarrow {{e}^{2}}=\dfrac{36-16}{36} \\\ & \Rightarrow {{e}^{2}}=\dfrac{5}{9} \\\ & \therefore e=\dfrac{\sqrt{5}}{3} \\\ \end{aligned}$
Therefore, the length between the two foci (say, d) can be calculated as follows:
$\begin{aligned} & \Rightarrow d=2ae \\\ & \Rightarrow d=2\times 6\times \dfrac{\sqrt{5}}{3}cm \\\ & \therefore d=4\sqrt{5}cm \\\ \end{aligned}$
This ellipse can be constructed as follows:

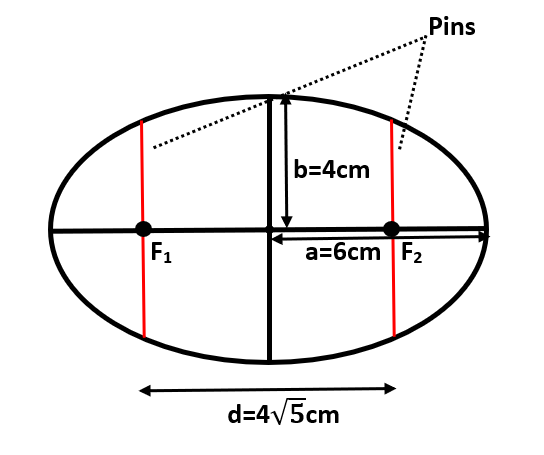
Here, we can clearly see the pins pinned down at ${{F}_{1}}\text{ and }{{F}_{2}}$and the characteristic ellipse formed around it with string.
Hence, the necessary length of string is $31.4cm$ and the distance between the two pins is equal to $4\sqrt{5}cm$.

Note: One should be able to visualize the construction of these mathematical figures with the help of the statement given in the problem. Also, one important criteria of the eccentricity of an ellipse is that it is always less than 1. And, for eccentricity equals to 1, we get a circle. This means, all circles are ellipse but all ellipses are not necessarily a circle.