Question

An ellipse has OB as semi-minor axis, F and F’ its foci and the $\angle FBF'$ is a right angle. Then, the eccentricity of the ellipse is
(A) $\dfrac{1}{\sqrt{3}}$
(B) $\dfrac{1}{4}$
(C) $\dfrac{1}{2}$
(D) $\dfrac{1}{\sqrt{2}}$

Answer 1

Assume an ellipse with F and F’ as its foci, the length of the major and minor axes are $a$ and
$b$ respectively. We know the property of the ellipse that the coordinates of its foci are $\left( -ae,0 \right)$ and $\left( ae,0 \right)$ . In $\Delta BOF$ and $\Delta BOF'$ , apply the formula $\tan \theta =\dfrac{Perpendicular}{Base}$ for $\angle BFO$ and
$\angle BF'O$ . Since it is given that BF and BF’ are perpendicular to each other and we know the property that the product of the slope of two perpendicular lines is -1. Now, apply this property for the lines BF and BF’, and obtain the relation between $a$ , $b$ , and $e$ . At last, use the formula for the eccentricity of ellipse, $e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$ and calculate the value of $e$ .

Complete step by step answer:
According to the question, we are given an ellipse that has OB as semi-minor axis, F and F’ its foci and the $\angle FBF'$ is a right angle.
Let us assume an ellipse with F and F’ as its foci, the length of the major and minor axes are $a$ and
$b$ respectively …………………………………………(1)
We know the property of the ellipse that the coordinates of its foci are $\left( -ae,0 \right)$ and $\left( ae,0 \right)$ ……………………………………………(2)
Here, F and F’ are the foci of the given ellipse …………………………………….……(3)
Now, from equation (2) and equation (3), we get
The coordinate of the focus F = $\left( ae,0 \right)$ ……………………………………..(4)
The coordinate of the focus F’ = $\left( -ae,0 \right)$ ……………………………………..(5)
Now, let us draw the diagram of the ellipse for the given information.

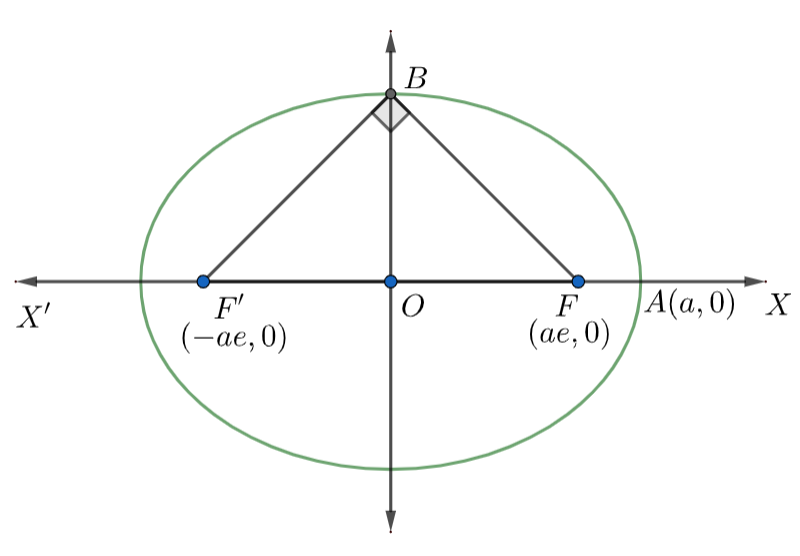
In the above diagram, we can observe that
$\angle BFX+\angle BFO=180{}^\circ$ (linear pair)
$\angle BFX=180{}^\circ -\angle BFO$ ……………………………………………(6)
Similarly, $\angle BF'X+\angle BF'O=180{}^\circ$ (linear pair)
$\angle BF'X=180{}^\circ -\angle BF'O$ ……………………………………………(7)
Now, in $\Delta BOF$ , we have
Perpendicular = OB = $b$ (length of minor axis) ………………………………(8)
Base = OF = $ae$ (from the diagram) …………………………………….(9)
We also know that $\tan \theta =\dfrac{Perpendicular}{Base}$ …………………………………..(10)
Now, from equation (8), equation (9), and equation (10), we get
$\tan \angle BFO=\dfrac{b}{ae}$ …………………………………………..(11)
Now, in $\Delta BOF'$ , we have
Perpendicular = OB = $b$ (length of minor axis) ………………………………(12)
Base = OF’ = $ae$ (from the diagram) …………………………………….(13)
Now, from equation (10), equation (12), and equation (13), we get
$\tan \angle BF'O=\dfrac{b}{ae}$ …………………………………………..(14)
The slope of line BF = $\tan \angle BFX$ ………………………………………….(15)
Now, from equation (6) and equation (15), we get
The slope of line BF = $\tan \left( 180{}^\circ -\angle BF0 \right)=-\tan \angle BFO$ ……………………………………..(16)
The slope of line BF’ = $\tan \angle BF'X$ ………………………………………….(17)
Now, from equation (7) and equation (17), we get
The slope of line BF’ = $\tan \angle BF'X=\tan \angle BF'O$ ……………………………………..(18)
Since it is given that BF and BF’ are perpendicular to each other and we know the property that the product of the slope of two perpendicular lines is -1 …………………………………………….(19)
Now, from equation (16), equation (18), and equation (19), we get
$\Rightarrow \left( -\tan \angle BFO \right)\times \left( \tan \angle BF'O \right)=-1$ ……………………………………(20)
Now, from equation (11), equation (14), and equation (20), we get

& \Rightarrow \left( -\dfrac{b}{ae} \right)\times \left( \dfrac{b}{ae} \right)=-1 \\\ & \Rightarrow \dfrac{{{b}^{2}}}{{{a}^{2}}{{e}^{2}}}=1 \\\ \end{aligned}$$ $$\Rightarrow {{b}^{2}}={{a}^{2}}{{e}^{2}}$$ ……………………………………..(21) We know the formula for the eccentricity of ellipse, $$e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$$ …………………………………….(22) Now, from equation (21) and equation (22), we get $$\begin{aligned} & \Rightarrow e=\sqrt{1-\dfrac{{{a}^{2}}{{e}^{2}}}{{{a}^{2}}}} \\\ & \Rightarrow {{e}^{2}}=1-{{e}^{2}} \\\ & \Rightarrow 2{{e}^{2}}=1 \\\ & \Rightarrow e=\sqrt{\dfrac{1}{2}} \\\ \end{aligned}$$ Therefore, the eccentricity of the ellipse is $$\dfrac{1}{\sqrt{2}}$$ . **So, the correct answer is “Option D”.** **Note:** For solving this question, we have to recall three points. The first one is that the coordinates of its foci are $$\left( -ae,0 \right)$$ and $$\left( ae,0 \right)$$. The second one is that the product of the slope of two perpendicular lines is -1. The third one is the formula for the eccentricity of ellipse, $$e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$$.