Question

An ellipse has OB as semi-minor axis, F and F’ are its foci and the angle FBF’ is a right angle then, the eccentricity of the ellipse is
$a.\dfrac{1}{{\sqrt 3 }} \\\ b.\dfrac{1}{4} \\\ c.\dfrac{1}{2} \\\ d.\dfrac{1}{{\sqrt 2 }} \\\$

Answer 1

In order to solve this problem we need to know that the Product of slopes of two perpendicular lines is -1. Drawing the diagram will help you a lot. You need to use the formula of eccentricity $e = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}}$. Doing this will solve this problem.

Complete step-by-step answer:
The figure to this problem can be drawn as,

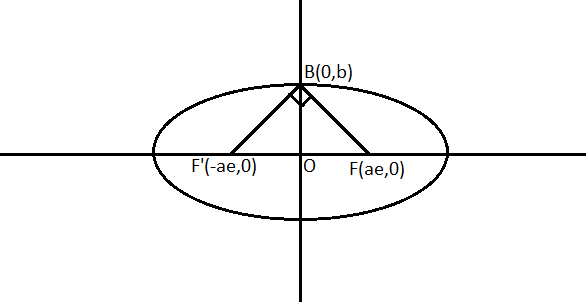
Let equation of ellipse is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$
We can easily see in figure coordinates of B(0, b), F (ae, 0) and F’(-ae, 0).
We know, F’B perpendicular to FB.
Thus, Product of slopes of two perpendicular lines is -1.
So, slope of F’B x slope of FB = -1
Slope of F’B = $\dfrac{{b - 0}}{{0 + ae}} = \dfrac{b}{{ae}}$
Slope of FB = $\dfrac{{b - 0}}{{0 - ae}} = \dfrac{{ - b}}{{ae}}$
$\Rightarrow \dfrac{b}{{ae}} \times \dfrac{{ - b}}{{ae}} = - 1$ (When we multiply the slopes of two perpendicular lines)
$\Rightarrow \dfrac{{ - {b^2}}}{{{a^2}{e^2}}} = - 1$
On solving we get,
${b^2} = {a^2}{e^2}$…..(1)
We know that $e = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}}$
Now, put the value of ${b^2}$ from (1) equation in (2) equation.
We get the new equation as,
$\Rightarrow e = \sqrt {1 - \dfrac{{{a^2}{e^2}}}{{{a^2}}}} \\\ \Rightarrow e = \sqrt {1 - {e^2}} \\\$
On squaring both sides we get,
$\Rightarrow {e^2} = 1 - {e^2}$
On further solving the equations we get,
$\Rightarrow 2{e^2} = 1 \\\ \Rightarrow e = \dfrac{1}{{\sqrt 2 }} \\\$

So, the correct answer is “Option d”.

Note: Whenever we face such types of problems we use some important points. Like first of all draw a figure and mark coordinates then find the value of slope of lines using coordinates and as we know the product of slopes of two perpendicular lines always be -1. Knowing this will solve our problem and will give you the right answer.